练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知z1=1-i，z2=2+2i．
    （1）求z1•z2；
    （2）若z=$\frac{{z}_{1}•{z}_{2}}{{z}_{1}+{z}_{2}}$，求z．

    分析 直接利用复数代数形式的乘法运算化简得答案．

    解答 解：（1）z1=1-i，z2=2+2i则z1•z2=（1-i）（2+2i）=4，
    （2）z1+z2=1-i+2+2i=3+i，
    ∴z=$\frac{{z}_{1}•{z}_{2}}{{z}_{1}+{z}_{2}}$=$\frac{4}{3+i}$=$\frac{4（3-i）}{（3+i）（3-i）}$=$\frac{6-2i}{5}$

    点评 本题考查了复数代数形式的乘法运算，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．若单位向量$\overrightarrow{e_1}$，$\overrightarrow{e_2}$的夹角为$\frac{π}{3}$，则向量$\overrightarrow{e_1}-2\overrightarrow{e_2}$与向量$\overrightarrow{e_1}$的夹角为（　　）
    A．$\frac{π}{2}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．集合M={（x，y）|x+y≤1，y≤x，y≥-1}，N={（x，y）|（x-2）2+y2=r2，r＞0}，若M∩N≠∅，则r的取值范围为（　　）
    A．$[{\frac{{\sqrt{2}}}{2}，3}]$B．$[{1，\sqrt{10}}]$C．$[{\frac{{\sqrt{2}}}{2}，\sqrt{10}}]$D．$[{1，\frac{{\sqrt{10}}}{2}}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=x3+$\frac{1}{x+1}$，x∈[0，1]．
    （1）用分析法证明：f（x）≥1-x+x2；
    （2）证明：f（x）＞$\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知复数z=3+4i，则|z|等于（　　）
    A．25B．12C．7D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．过双曲线x2-y2=1焦点的直线垂直于x轴，交双曲线于A、B两点，则|AB|=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．在△ABC中，a，b，c分别为角A，B，C所对的边，若b=$\sqrt{2}$，a=2，B=$\frac{π}{4}$，则c=（　　）
    A．$\frac{1}{2}$B．$\sqrt{2}$C．2D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

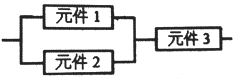    16．某个部件由三个元件按图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作（其中元件1，2，3正常工作的概率都为$\frac{1}{2}$），设三个电子元件的使用寿命（单位：小时）均服从正态分布N（1000，502），且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为（　　）
    A．$\frac{3}{4}$B．$\frac{1}{4}$C．$\frac{5}{8}$D．$\frac{3}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．在△ABC中，B=45°，C=60°，c=2，则b=（　　）
    A．$\frac{{2\sqrt{6}}}{3}$B．$\frac{{3\sqrt{6}}}{2}$C．$\frac{1}{2}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    同步练习册答案