
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 可知$|\overrightarrow{{e}_{1}}|=|\overrightarrow{{e}_{2}}|=1,<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>=\frac{π}{3}$,这样进行数量积的运算即可求出$(\overrightarrow{{e}_{1}}-2\overrightarrow{{e}_{2}})•\overrightarrow{{e}_{1}}=0$,这样即可得出向量$\overrightarrow{{e}_{1}}-2\overrightarrow{{e}_{2}}$与向量$\overrightarrow{{e}_{1}}$的夹角.
解答 解:$(\overrightarrow{{e}_{1}}-2\overrightarrow{{e}_{2}})•\overrightarrow{{e}_{1}}={\overrightarrow{{e}_{1}}}^{2}-2\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=$1-2×\frac{1}{2}=0$;
∴$(\overrightarrow{{e}_{1}}-2\overrightarrow{{e}_{2}})⊥\overrightarrow{{e}_{1}}$;
∴向量$\overrightarrow{{e}_{1}}-2\overrightarrow{{e}_{2}}$与$\overrightarrow{{e}_{1}}$的夹角为$\frac{π}{2}$.
故选A.
点评 考查单位向量的概念,向量数量积的运算及计算公式,向量夹角的概念.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
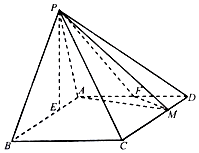 在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,AD=2$\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.
在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,AD=2$\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).| 工种类别 | A | B | C |
| 赔付频率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
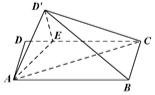 如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 75%,170 | B. | 75%,340 | C. | 25%,170 | D. | 25%,340 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
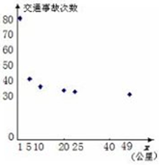 经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |
| $\overline{y}$ $\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(1)})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(2)})^{2}$ |
| 41.7 1821 | 0.875 | 48.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com