
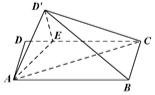
 如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.分析 (Ⅰ)连接BD交AE于点O,推导出Rt△ABD~Rt△DAE,从而得到OB⊥AE,OD'⊥AE,由此能证明AE⊥平面OBD'.
(Ⅱ)由VA-BCD'=VD'-ABC,能求出三棱锥A-BCD'的体积.
解答 证明:(Ⅰ)连接BD交AE于点O,依题意得$\frac{AB}{DA}=\frac{AD}{DE}=2$,
所以Rt△ABD~Rt△DAE,
所以∠DAE=∠ABD,所以∠AOD=90°,所以AE⊥BD,
即OB⊥AE,OD'⊥AE,又OB∩OD′=O,
OB,OD'?平面OBD'.
所以AE⊥平面OBD'.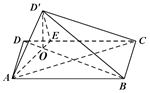
解:(Ⅱ)因为平面AD'E⊥平面ABCE,
由(Ⅰ)知,OD'⊥平面ABCE,
所以OD'为三棱锥D'-ABC的高,
在矩形ABCD中,AB=4,AD=2,DE=1,所以$D'O=\frac{2}{{\sqrt{5}}}$,
所以VA-BCD'=VD'-ABC=$\frac{1}{3}{S_{△ABC}}•D'O$=$\frac{1}{3}×({\frac{1}{2}×4×2})×\frac{2}{{\sqrt{5}}}=\frac{{8\sqrt{5}}}{15}$
即三棱锥A-BCD'的体积为$\frac{{8\sqrt{5}}}{15}$.
点评 本题考查几何体的体积及直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查考查推理论证能力、运算求解能力、空间想象能力,考查化归转化思想、函数与方程思想,数形结合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-ln2,0)∪(3,+∞) | B. | (-ln2,+∞) | C. | (3,+∞) | D. | (-ln2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
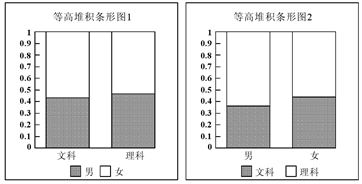
| A. | 样本中的女生数量多于男生数量 | |
| B. | 样本中有理科意愿的学生数量多于有文科意愿的学生数量 | |
| C. | 样本中的男生偏爱理科 | |
| D. | 样本中的女生偏爱文科 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |
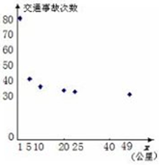
| $\overline{x}$ | $\overline{y}$ $\overline{ω}$ $\overline{φ}$ | $\sum_{i=1}^{6}({ω}_{i}-\overline{ω})^{2}$ | $\sum_{i=1}^{6}({φ}_{i}-\overline{φ})^{2}$ | $\sum_{i=1}^{6}({ω}_{i}-\overline{ω})({y}_{i}-\overline{y})$ | $\sum_{i=1}^{6}({φ}_{i}-\overline{φ})({y}_{i}-\overline{y})$ |
| 18.3 | 41.7 0.235 0.062 | 0.723 | 0.112 | 36.3 | 14.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com