
| �������� 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
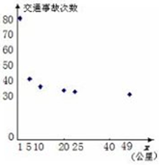
| ��ͨ�¹��� 80 | 40 | 35 | 33 | 32 | 30 |
| $\overline{x}$ | $\overline{y}$ $\overline{��}$ $\overline{��}$ | $\sum_{i=1}^{6}��{��}_{i}-\overline{��}��^{2}$ | $\sum_{i=1}^{6}��{��}_{i}-\overline{��}��^{2}$ | $\sum_{i=1}^{6}��{��}_{i}-\overline{��}����{y}_{i}-\overline{y}��$ | $\sum_{i=1}^{6}��{��}_{i}-\overline{��}����{y}_{i}-\overline{y}��$ |
| 18.3 | 41.7 0.235 0.062 | 0.723 | 0.112 | 36.3 | 14.1 |
���� ����ȡy=a+$\frac{b}{x}$�������ع鷽�̣���y=a+b�أ�����ع�ϵ�������ɵó����ۣ�
����1040����ȡx=40����y��1��=29.9+50.2��$\frac{1}{40}$��31.16��ÿ�ν�ͨ�¹ʵ������=60��0.01+2��0.19+0.2��0.8=1��14��Ԫ�����ɵó����ۣ�
��� �⣺����ȡy=a+$\frac{b}{x}$�������ع鷽�̣���y=a+b�أ�b=$\frac{36.3}{0.723}$��50.2��
��a=41.7-50.2��0.235��29.9��
��y=29.9+50.2�أ���y=29.9+50.2��$\frac{1}{x}$��
����1040����ȡx=40����y��1��=29.9+50.2��$\frac{1}{40}$��31.16��ÿ�ν�ͨ�¹ʵ������=60��0.01+2��0.19+0.2��0.8=1��14��Ԫ��
��Ԥ����һ���ڽ�1040���︽���������Ľ�ͨ�¹ʵ������Ϊ31.16��1.14��35.5��Ԫ��
���� ���⿼��ع鷽�̣�����������ѧ֪ʶ���ʵ�����������������ѧ���ļ��������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��3�� | B�� | [-1��3] | C�� | ��-3��1�� | D�� | [-3��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
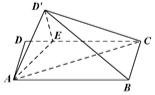 ��ͼ������ABCD�У�AB=4��AD=2��E��DC���ϣ���DE=1������ADE��AE�۵���AD'E��λ�ã�ʹ��ƽ��AD'E��ƽ��ABCE��
��ͼ������ABCD�У�AB=4��AD=2��E��DC���ϣ���DE=1������ADE��AE�۵���AD'E��λ�ã�ʹ��ƽ��AD'E��ƽ��ABCE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 75%��170 | B�� | 75%��340 | C�� | 25%��170 | D�� | 25%��340 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20 | B�� | 10 | C�� | 5 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͳ�ƣ�2015�꣬ij��·�ڲ��ֽ����������Ľ�ͨ�¹ʴ������±���
��ͳ�ƣ�2015�꣬ij��·�ڲ��ֽ����������Ľ�ͨ�¹ʴ������±���| �������� 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| ��ͨ�¹��� 80 | 40 | 35 | 33 | 32 | 30 |
| $\overline{y}$ $\sum_{i=1}^{6}��{y}_{i}-\overline{y}��^{2}$ | $\sum_{i=1}^{6}��{y}_{i}-{\widehat{{y}_{i}}}^{��1��}��^{2}$ | $\sum_{i=1}^{6}��{y}_{i}-{\widehat{{y}_{i}}}^{��2��}��^{2}$ |
| 41.7 1821 | 0.875 | 48.4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 26 | B�� | 24 | C�� | 20 | D�� | 13 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com