
分析 (1)利用分析法的证明步骤,即可得出结论.
(2)利用配方法,结合(1),即可得出结论.
解答 证明:(1)∵x∈[0,1],∴x+1∈[1,2].
要证明:f(x)≥1-x+x2,
只要证明:x3(x+1)+1≥(x+1)(1-x+x2),
只要证明:x4≥0,
显然成立,
∴f(x)≥1-x+x2;
(2)∵1-x+x2=(x-$\frac{1}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$,当且仅当x=$\frac{1}{2}$时取等号,
∵f($\frac{1}{2}$)=$\frac{19}{24}$>$\frac{3}{4}$,f(x)≥1-x+x2,
∴f(x)>$\frac{3}{4}$.
点评 本题主要考查用分析法证明不等式,把证明不等式转化为寻找使不等式成立的充分条件,直到使不等式成立的充分条件显然已经具备为止.


科目:高中数学 来源: 题型:解答题
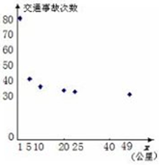 经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |
| $\overline{y}$ $\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(1)})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(2)})^{2}$ |
| 41.7 1821 | 0.875 | 48.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosx-sinx | B. | sinx-cosx | C. | sinx+cosx | D. | -sinx-cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 简单随机抽样 | B. | 系统抽样 | C. | 分层抽样 | D. | 抽签法 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 26 | B. | 24 | C. | 20 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com