
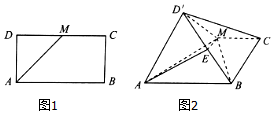
 如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.分析 (Ⅰ)推导出∠AMB=90°,D'A⊥BM,从而BM⊥面D'AM,由此能证明面ABCM⊥面D'AM.
(Ⅱ)在平面D'AM内过M作直线NM⊥MA,以M为原点,$\overrightarrow{MA},\overrightarrow{MB},\overrightarrow{MN}$分别为x,y,z轴的正方向建立空间直角坐标系,利用向量法能求出二面角E-AM-D'的余弦值.
解答 证明:(Ⅰ)由题知,在矩形ABCD中,∠AMD=∠BMC=45°,
∴∠AMB=90°,
又D'A⊥BM,∴BM⊥面D'AM,
∵BM?面ABCM,
∴面ABCM⊥面D'AM;
解:(Ⅱ)由(Ⅰ)知,在平面D'AM内过M作直线NM⊥MA,则NM⊥平面ABCM,
故以M为原点,$\overrightarrow{MA},\overrightarrow{MB},\overrightarrow{MN}$分别为x,y,z轴的正方向建立空间直角坐标系,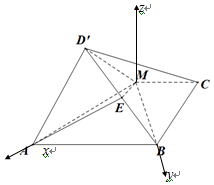
则M(0,0,0),A(2,0,0),B(0,2,0),D'(1,0,1),
于是$E(\frac{1}{2},1,\frac{1}{2})$,$\overrightarrow{MA}=(2,0,0)$,$\overrightarrow{ME}=(\frac{1}{2},1,\frac{1}{2})$,
设平面EAM的法向量为$\overrightarrow m=(x,y,z)$,
则$\left\{\begin{array}{l}2x=0\\ \frac{1}{2}x+y+\frac{1}{2}z=0\end{array}\right.$令y=1,得平面EAM的一个法向量$\overrightarrow m=(0,1,-2)$,
平面D'AM的一个法向量为$\overrightarrow n=(0,1,0)$,
故$cos<\overrightarrow m,\overrightarrow n>=\frac{1}{{\sqrt{5}}}$,
即二面角E-AM-D'的余弦值为$\frac{{\sqrt{5}}}{5}$.
点评 本题考查二面角及直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查考查推理论证能力、运算求解能力、空间想象能力,考查化归转化思想,数形结合思想,是中档题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $-\frac{4\sqrt{2}}{9}$ | C. | $-\frac{7}{9}$ | D. | $±\frac{4\sqrt{2}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1980 | B. | 4096 | C. | 5904 | D. | 8020 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{m-1}{m+1}$ | B. | $\frac{m}{m+1}$ | C. | $\frac{m-1}{m}$ | D. | $\frac{{2\sqrt{m}}}{m+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
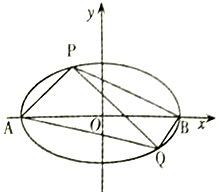 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com