
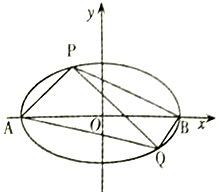
 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.分析 (Ⅰ)由题意求得椭圆方程,则kAP=$\frac{y-0}{x+2}$,kBP=$\frac{y-0}{x-2}$,即可求得kAP•kBP=-$\frac{1}{2}$,由kBQ=2kAP,故kBP•kBQ=-1;
(Ⅱ)设直线l的方程,代入椭圆方程,由韦达定理,及向量数量积的坐标运算,求得直线恒过点$(\frac{2}{3},0)$,则${S_{△APQ}}={S_{△APM}}+{S_{△AQM}}=\frac{1}{2}×|OM|×|{y_1}-{y_2}|$,根据函数的单调性即可求得三角形APQ的面积S的最大值,当直线lPQ的斜率k不存在时,根据斜率关系,求得P和Q方程,即可求得三角形APQ的面积S.
解答 解:(Ⅰ)证明:由椭圆的离心率e=$\frac{c}{a}$=$\frac{{\sqrt{2}}}{2}$,则a=$\sqrt{2}$c,
由焦点到短轴端点的距离为2,即a=2,则c=$\sqrt{2}$,
b2=a2-c2=2,
∴椭圆的标准方程为:$\frac{x^2}{4}+\frac{y^2}{2}=1$;
设P点坐标(x,y),y2=$\frac{1}{2}$(4-x2)则A(-2,0),B(2,0),则kAP=$\frac{y-0}{x+2}$,kBP=$\frac{y-0}{x-2}$,
则kAP•kBP=$\frac{{y}^{2}}{{x}^{2}-4}$=-$\frac{1}{2}$
由kBQ=2kAP,故kBP•kBQ=-1.
∴直线BP与直线BQ的斜率乘积为-1为定值;
(Ⅱ)当直线PQ的斜率存在时,设lPQ:y=kx+b与x轴的交点为M,
$\left\{\begin{array}{l}{y=kx+b}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,整理得:(2k2+1)x2+4kbx+2b2-4=0,
设P(x1,y1),Q(x2,y2),则${x_1}+{x_2}=\frac{-4kb}{{2{k^2}+1}}$,${x_1}{x_2}=\frac{{2{b^2}-4}}{{2{k^2}+1}}$,
由$\overrightarrow{BP}•\overrightarrow{BQ}=0$,得y1y2+x1x2-2(x1+x2)+4=0,
得$({k^2}+1){x_1}{x_2}+(kb-2)({x_1}+{x_2})+4+{b^2}=0$,
4k2+8kb+3b2=0,得b=-2k或$b=-\frac{2}{3}k$.y=kx-2k或$y=kx-\frac{2}{3}k$,
所以过定点(2,0)或$(\frac{2}{3},0)$,
点(2,0)为右端点,舍去,
${S_{△APQ}}={S_{△APM}}+{S_{△AQM}}=\frac{1}{2}×|OM|×|{y_1}-{y_2}|$,
=$\frac{8}{3}\sqrt{\frac{{{k^2}(8{k^2}-2{b^2}+4)}}{{{{(2{k^2}+1)}^2}}}}=\frac{16}{9}\sqrt{\frac{{{k^2}(16{k^2}+9)}}{{{{(2{k^2}+1)}^2}}}}$,
=$\frac{16}{9}\sqrt{4-\frac{7}{2}[{\frac{1}{{2{k^2}+1}}+\frac{1}{{2{{(2{k^2}+1)}^2}}}}]}$,
令$\frac{1}{{2{k^2}+1}}=t$(0<t<1),${S_{△APQ}}=\frac{16}{9}\sqrt{4-\frac{7}{2}(t+\frac{1}{2}{t^2})}$,0<t+t2<1,${S_{△APQ}}<\frac{32}{9}$,
当直线lPQ的斜率k不存在时,P(x1,y1),Q(x1,-y1),${k_{AP}}=\frac{1}{2}{k_{BQ}}$,即$\frac{{2{y_1}}}{{{x_1}+2}}=\frac{{-{y_1}}}{{{x_1}-2}}$,
解得${x_1}=\frac{2}{3}$,${y_1}=\frac{4}{3}$,${S_{△APQ}}=\frac{1}{2}×\frac{8}{3}×\frac{8}{3}=\frac{32}{9}$,
∴S△APQ的最大值为$\frac{32}{9}$.
点评 本题考查椭圆的标准方程及简单性质,直线与椭圆的位置关系,考查韦达定理,弦长公式,函数单调性及最值与椭圆的综合应用,考查分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
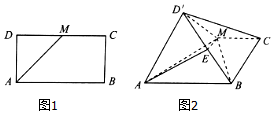 如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-ln2,0)∪(3,+∞) | B. | (-ln2,+∞) | C. | (3,+∞) | D. | (-ln2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
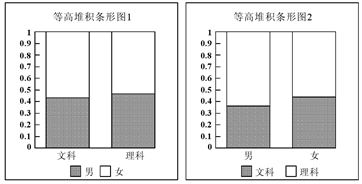
| A. | 样本中的女生数量多于男生数量 | |
| B. | 样本中有理科意愿的学生数量多于有文科意愿的学生数量 | |
| C. | 样本中的男生偏爱理科 | |
| D. | 样本中的女生偏爱文科 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
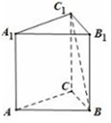
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 132 | B. | 180 | C. | 240 | D. | 600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com