
分析 先根据正态分布曲线的图象特征,关注其对称性画出函数的图象,观察图象在80分到120分之间的人数概率,即可得成绩不低于120分的学生人数概率,最后即可求得成绩不低于120分的学生数.
解答 解:∵成绩ξ~N(100,a2),
∴其正态曲线关于直线x=100对称,
又∵成绩在80分到120分之间的人数约为总人数的60%,
由对称性知:成绩在120分以上的人数约为总人数的$\frac{1}{2}(1-0.6)$=0.2,
∴此次数学考试成绩不低于120分的学生约有:0.2×1000=200.
故答案为:200.
点评 本小题主要考查正态分布曲线的特点及曲线所表示的意义等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $-\frac{4\sqrt{2}}{9}$ | C. | $-\frac{7}{9}$ | D. | $±\frac{4\sqrt{2}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
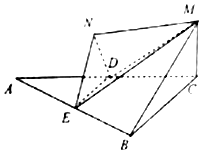 已知如图,△ABC是边长为4的等边三角形,MC⊥平面ABC,D、E分别是线段AC、AB的中点,将△ADE沿DE翻折至△NDE,平面NDE⊥平面ABC.
已知如图,△ABC是边长为4的等边三角形,MC⊥平面ABC,D、E分别是线段AC、AB的中点,将△ADE沿DE翻折至△NDE,平面NDE⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{10}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1980 | B. | 4096 | C. | 5904 | D. | 8020 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
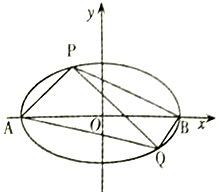 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com