
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 先化简f(x),再根据函数的图象关于y轴对称,求出φ的值,再根据余弦函数的图象求出最值
解答 解:f(x)=$\sqrt{3}$sin(2x-φ)-cos(2x-φ)=2sin(2x-φ-$\frac{π}{6}$),
∵f(x)图象关于y轴对称,
∴φ+$\frac{π}{6}$=$\frac{π}{2}$,
∴φ=$\frac{π}{3}$,
∴f(x)=2sin(2x-$\frac{π}{2}$)=-2cos2x,
∵x∈$[{-\frac{π}{6},\frac{π}{3}}]$,
∴函数f(x)在[-$\frac{π}{6}$,0]上递减,在[0,$\frac{π}{3}$]上单调递增,
∴f(-$\frac{π}{6}$)=-2cos(-$\frac{π}{3}$)=-1,f($\frac{π}{3}$)=-2cos$\frac{2π}{3}$=1,
∴f(x)在区间$[{-\frac{π}{6},\frac{π}{3}}]$上的最大值为1,
故选:A
点评 本题考查了三角函数的化简,以及余弦函数的性质,属于中档题


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
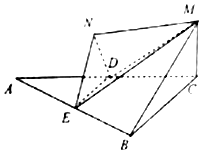 已知如图,△ABC是边长为4的等边三角形,MC⊥平面ABC,D、E分别是线段AC、AB的中点,将△ADE沿DE翻折至△NDE,平面NDE⊥平面ABC.
已知如图,△ABC是边长为4的等边三角形,MC⊥平面ABC,D、E分别是线段AC、AB的中点,将△ADE沿DE翻折至△NDE,平面NDE⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1980 | B. | 4096 | C. | 5904 | D. | 8020 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{m-1}{m+1}$ | B. | $\frac{m}{m+1}$ | C. | $\frac{m-1}{m}$ | D. | $\frac{{2\sqrt{m}}}{m+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
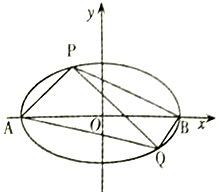 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos2θ | B. | 1 | C. | cos2θ | D. | cos2θ+isinθ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com