
分析 (Ⅰ)f'(x)=aex-(1+lnx),f(x)是(0,+∞)上的增函数等价于f'(x)≥0恒成立.令f'(x)≥0,得$a≥\frac{1+lnx}{e^x}$,令$g(x)=\frac{1+lnx}{e^x}$(x>0),求导得$g'(x)={e^{-x}}({\frac{1}{x}-1-lnx})$,令$h(x)=\frac{1}{x}-1-lnx$,$h'(x)=-\frac{1}{x^2}-\frac{1}{x}<0$,由此能求出a的取值范围.
(Ⅱ)f(x)>0?$\frac{{a{e^x}}}{x}-lnx>0$.令F(x)=$\frac{a{e}^{x}}{x}-lnx$(x>0),当$a≥\frac{2}{e^2}$时,F(x)的最小值大于0.由此利用导数性质能证明当$a≥\frac{2}{e^2}$时,总有f(x)>0.
解答 解:(Ⅰ)f'(x)=aex-(1+lnx),f(x)是(0,+∞)上的增函数等价于f'(x)≥0恒成立.
令f'(x)≥0,得$a≥\frac{1+lnx}{e^x}$,令$g(x)=\frac{1+lnx}{e^x}$(x>0).以下只需求g(x)的最大值.
求导得$g'(x)={e^{-x}}({\frac{1}{x}-1-lnx})$,
令$h(x)=\frac{1}{x}-1-lnx$,$h'(x)=-\frac{1}{x^2}-\frac{1}{x}<0$,h(x)是(0,+∞)上的减函数,
又h(1)=0,故1是h(x)的唯一零点,
当x∈(0,1),h(x)>0,g'(x)>0,g(x)递增;
当x∈(1,+∞),h(x)<0,g'(x)<0,g(x)递减;
故当x=1时,g(x)取得极大值且为最大值$g(1)=\frac{1}{e}$,
所以$a≥\frac{1}{e}$,即a的取值范围是$[{\frac{1}{e},+∞})$.
证明:(Ⅱ)f(x)>0?$\frac{{a{e^x}}}{x}-lnx>0$.
令F(x)=$\frac{a{e}^{x}}{x}-lnx$(x>0),以下证明当$a≥\frac{2}{e^2}$时,F(x)的最小值大于0.
求导得$F'(x)=\frac{{a({x-1}){e^x}}}{x^2}-\frac{1}{x}$=$\frac{1}{x^2}[{a({x-1}){e^x}-x}]$.
①当0<x≤1时,F'(x)<0,F(x)≥F(1)=ae>0;
②当x>1时,$F'(x)=\frac{{a({x-1})}}{x^2}$$[{{e^x}-\frac{x}{{a({x-1})}}}]$,令$G(x)={e^x}-\frac{x}{{a({x-1})}}$,
则G'(x)=ex$+\frac{1}{{a{{({x-1})}^2}}}>0$,又$G(2)={e^2}-\frac{2}{a}$=$\frac{{a{e^2}-2}}{a}≥0$,
取m∈(1,2)且使$\frac{m}{{a({m-1})}}>{e^2}$,即$1<m<\frac{{a{e^2}}}{{a{e^2}-1}}$,则$G(m)={e^m}-\frac{m}{{a({m-1})}}$<e2-e2=0,
因为G(m)G(2)<0,故G(x)存在唯一零点x0∈(1,2),
即F(x)有唯一的极值点且为极小值点x0∈(1,2),又$F({x_0})=\frac{{a{e^{x_0}}}}{x_0}-ln{x_0}$,
且$G({x_0})={e^{x_0}}-\frac{x_0}{{a({{x_0}-1})}}=0$,即${e^{x_0}}=\frac{x_0}{{a({{x_0}-1})}}$,故$F({x_0})=\frac{1}{{{x_0}-1}}-ln{x_0}$,
因为$F'({x_0})=-\frac{1}{{{{({{x_0}-1})}^2}}}-\frac{1}{x_0}<0$,故F(x0)是(1,2)上的减函数.
所以F(x0)>F(2)=1-ln2>0,所以F(x)>0.
综上,当$a≥\frac{2}{e^2}$时,总有f(x)>0.
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
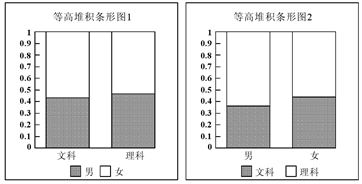
| A. | 样本中的女生数量多于男生数量 | |
| B. | 样本中有理科意愿的学生数量多于有文科意愿的学生数量 | |
| C. | 样本中的男生偏爱理科 | |
| D. | 样本中的女生偏爱文科 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
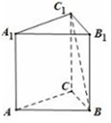
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com