
分析 (1)通过去掉绝对值符号化简不等式求解即可.
(2)利用基本不等式求解最值,利用绝对值不等式的几何意义转化恒成立不等式求解a的范围即可.
解答 解:(1)不等式2f(x)<4-|x-1|等价于2|x+2|+|x-1|<4,即$\left\{\begin{array}{l}x≤-2\\-2({x+2})-x+1<4\end{array}\right.$或$\left\{\begin{array}{l}-2<x<1\\ 2({x+2})-x+1<4\end{array}\right.$或$\left\{\begin{array}{l}x≥1\\ 2({x+2})+x-1<4\end{array}\right.$.解得$\left\{{x|-\frac{7}{3}<x≤-2}\right\}$或{x|-2<x-1}或∅,
所以不等式的解集为$\left\{{x|-\frac{7}{3}<x<-1}\right\}$.
(2)因为|x-a|-f(x)=|x-a|-|x+2|≤|x-a-x-2|=|a+2|,所以|x-a|-f(x)的最大值是|a+2|,
又m+n=1(m>0,n>0),于是$({\frac{1}{m}+\frac{1}{n}})({m+n})=\frac{n}{m}+\frac{m}{n}+2≥2+2=4$,∴$\frac{1}{m}+\frac{1}{n}$的最小值为4.
要使$|{x-a}|-f(x)≤\frac{1}{m}+\frac{1}{n}$的恒成立,则|a+2|≤4,解此不等式得-6≤a≤2.
所以实数a的取值范围是[-6,2].
点评 本题考查绝对值不等式的解法,基本不等式的应用,函数恒成立的应用,考查计算能力.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{9}$,$\frac{4}{9}$] | B. | [$\frac{1}{9}$,$\frac{1}{4}$] | C. | [$\frac{2}{9}$,$\frac{1}{2}$] | D. | [$\frac{2}{9}$,$\frac{1}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
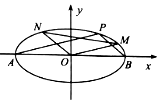 已知A,B分别为椭圆C:$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点,P为椭圆C上异于A,B两点的任意一点,直线PA,PB的斜率分别记为k1,k2.
已知A,B分别为椭圆C:$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点,P为椭圆C上异于A,B两点的任意一点,直线PA,PB的斜率分别记为k1,k2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 班级 | 1 | 2 | 3 | 4 | 5 |
| 数学(x分) | 111 | 113 | 119 | 125 | 127 |
| 物理(y分) | 92 | 93 | 96 | 99 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com