
分析 随着x的增大,指数函数的增长速度越来越快,当运动的时间足够长,最前面的动物一定是按照指数函数运动的物体,即一定是第四种物体.
解答 解:路程fi(x)(i=1,2,3,4)关于时间x(x>1)的函数关系是:
f1(x)=x2,f2(x)=2x,f3(x)=log2x,f4(x)=2x,
它们相应的函数模型分别是幂函数,一次函数,对数函数和指数函数模型.
根据四种函数的变化特点,随着x的增大,指数函数的增长速度越来越快,
当运动的时间足够长,最前面的物体一定是按照指数函数运动的物体,即一定是第四种物体,
∴最终在最前面的物体具有的函数关系是f4(x)=2x,
故答案为:f4(x)=2x .
点评 本题考查几种基本初等函数的变化趋势,关键是注意到对数函数、指数函数与幂函数的增长差异,属于基础题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
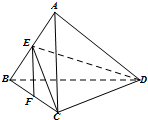 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E,F分别是AB,BC的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E,F分别是AB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“幂函数f(x)=(m2-m-1)xm在(0,+∞)上为增函数,则m=-1”为真命题 | |
| C. | 命题“若x=y则sinx=siny”的逆否命题为真命题 | |
| D. | 命题“?x0∈R,x02+x0+1<0”的否定是“?x∈R,x2+x+1>0” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com