
分析 通过计算出前几项的值确定周期,进而计算可得结论.
解答 解:依题意,a2=$\frac{1+{a}_{1}}{1-{a}_{1}}$=$\frac{1+\frac{1}{2}}{1-\frac{1}{2}}$=3,
a3=$\frac{1+{a}_{2}}{1-{a}_{2}}$=$\frac{1+3}{1-3}$=-2,
a4=$\frac{1+{a}_{3}}{1-{a}_{3}}$=$\frac{1-2}{1+2}$=$-\frac{1}{3}$,
a5=$\frac{1+{a}_{4}}{1-{a}_{4}}$=$\frac{1+\frac{1}{3}}{1-\frac{1}{3}}$=2,
∴数列{an}是以4为周期的周期数列,
又∵2016=504×4,
∴a2016=a4=-$\frac{1}{3}$,
故答案为:-$\frac{1}{3}$.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
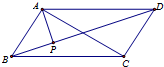 如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=2,则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8.
如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=2,则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥2 | B. | m≤2 | C. | m>2 | D. | -2<m<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d>p | B. | d<p | C. | d=p | D. | 无法比较 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com