
 ,
,  ,解关于x不等式
,解关于x不等式 ;
;(1)解:a= 时,求导函数可得
时,求导函数可得
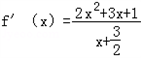 =
=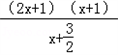 .
.
f(x)的定义域为(﹣ ,+∞).
,+∞).
当﹣ <x<﹣1时,f'(x)>0;
<x<﹣1时,f'(x)>0;
当﹣1<x<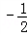 时,f'(x)<0;
时,f'(x)<0;
当x> 时,f'(x)>0.
时,f'(x)>0.
从而,f(x)在(﹣ ,﹣1),(
,﹣1),(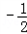 ,+∞)单调增加,在(﹣1,
,+∞)单调增加,在(﹣1,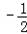 )单调减少.
)单调减少.
∵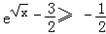 ,f(
,f( )=
)=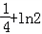
∴不等式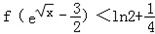 等价于
等价于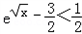
∴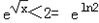
∴0≤x<ln22即所求不等式的解集为{x|0≤x<ln22}.
(2)证明:依题意,f(x)的定义域为(﹣a,+∞),
令g(x)=2x2+2ax+1,因为g(﹣a)=1=g(0)>0,
g(x)的对称轴为x=﹣0.5a>﹣a,△=4a2﹣8a>0(a2>2),g(﹣a)=1>0
∴g(x)在(﹣a,+∞)有两个零点.即方程2x2+2ax+1=0有两相异解
由已知f(x)的定义域为{x|x>﹣a}且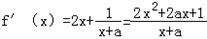 ,
,
若m,n(m>n)方程2x2+2ax+1=0有两相异解,则f'(x)>0的解集为(﹣a,n)∪(m,+∞)(∵a>0)



 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
| e | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2x |
| x+2 |
| 9 |
| 10 |
| 1 |
| e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 | x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| x |
| 3 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com