
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
分析 根据直线和圆相交的性质,结合充分条件和必要条件的定义进行判断即可得到结论.
解答 解:若直线l:y=kx+1与圆O:x2+y2=1相交于A,B 两点,
则圆心到直线距离d=$\frac{1}{\sqrt{1+{k}^{2}}}$,|AB|=2$\sqrt{1-{d}^{2}}=2\sqrt{1-\frac{1}{1+{k}^{2}}}=2\sqrt{\frac{{k}^{2}}{1+{k}^{2}}}$,
若k=1,则|AB|=$2\sqrt{\frac{1}{2}}=\sqrt{2}$,d=$\frac{1}{\sqrt{1+1}}=\frac{\sqrt{2}}{2}$,则△OAB的面积为$\frac{1}{2}$×$\sqrt{2}×\frac{\sqrt{2}}{2}$=$\frac{1}{2}$成立,即充分性成立.
若△OAB的面积为$\frac{1}{2}$,则S=$\frac{1}{2}×\frac{1}{\sqrt{1+{k}^{2}}}×2\sqrt{\frac{{k}^{2}}{1+{k}^{2}}}$=$\frac{1}{2}$×2×$\frac{|k|}{1+{k}^{2}}$=$\frac{|k|}{1+{k}^{2}}$=$\frac{1}{2}$,
即k2+1=2|k|,即k2-2|k|+1=0,
则(|k|-1)2=0,
即|k|=1,
解得k=±1,则k=1不成立,即必要性不成立.
故“k=1”是“△OAB的面积为$\frac{1}{2}$”的充分不必要条件.
故选:A.
点评 本题主要考查充分条件和必要条件的判断,利用三角形的面积公式,以及半径半弦之间的关系是解决本题的关键.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:解答题
 已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x,
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,5]∪[$\frac{19}{2}$,+∞) | B. | [5,8] | C. | [5,$\frac{19}{2}$] | D. | [8,$\frac{19}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
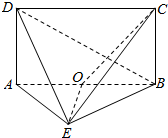 如图,多面体ABCDE中,ABCD是矩形,AB=2$\sqrt{2}$,BC=2,直线DA⊥平面ABE,AE=BE,O为棱AB的中点.
如图,多面体ABCDE中,ABCD是矩形,AB=2$\sqrt{2}$,BC=2,直线DA⊥平面ABE,AE=BE,O为棱AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com