
某人在C点测得某塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°方向前进10米到D,测得塔顶A的仰角为30°,则塔高为( )
(A)15米 (B)5米
(C)10米 (D)12米
C
【解析】【思路点拨】作出图形确定三角形,找到要用的角度和边长,利用余弦定理求得.
解:如图,设塔高为h米,在Rt△AOC中,∠ACO=45°,则OC=OA=h.
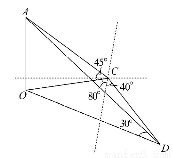
在Rt△AOD中,∠ADO=30°,则OD=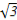 h,
h,
在△OCD中,∠OCD=120°,CD=10,
由余弦定理得:
OD2=OC2+CD2-2OC·CD·cos∠OCD,
即(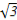 h)2=h2+102-2h×10×cos 120°,
h)2=h2+102-2h×10×cos 120°,
∴h2-5h-50=0,解得h=10或h=-5(舍去).
【方法技巧】测量高度的常见思路
解决高度的问题主要是根据条件确定出所利用的三角形,准确地理解仰角和俯角的概念并和三角形中的角度相对应;分清已知和待求的关系,正确地选择定理和公式,特别注意高度垂直地面构成的直角三角形.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十九第八章第十节练习卷(解析版) 题型:选择题
已知抛物线方程为y2=4x,直线l的方程为x-y+4=0,在抛物线上有一动点P到y轴的距离为d1,P到直线l的距离为d2,则d1+d2的最小值为( )
(A)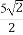 +2 (B)
+2 (B)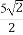 +1 (C)
+1 (C)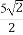 -2 (D)
-2 (D)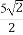 -1
-1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
若点A(3,5)关于直线l:y=kx的对称点在x轴上,则k是( )
(A) (B)±
(B)±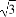
(C)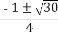 (D)
(D)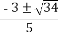
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十第三章第四节练习卷(解析版) 题型:选择题
如图,为了研究钟表与三角函数的关系,建立了如图所示的坐标系,设秒针针尖位置P(x,y).若初始位置为P0(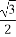 ,
, ),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
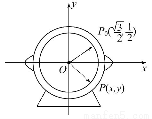
(A)y=sin(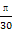 t+
t+ ) (B)y=sin(-
) (B)y=sin(-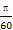 t-
t- )
)
(C)y=sin(-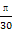 t+
t+ ) (D)y=sin(-
) (D)y=sin(-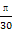 t-
t-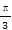 )
)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十四第三章第八节练习卷(解析版) 题型:解答题
在海岸A处,发现北偏东45°方向、距离A处(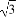 -1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10
-1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10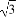 海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十四第三章第八节练习卷(解析版) 题型:选择题
某水库大坝的外斜坡的坡度为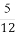 ,则坡角α的正弦值为( )
,则坡角α的正弦值为( )
(A)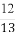 (B)
(B)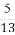 (C)
(C)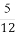 (D)
(D)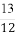
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十六第四章第二节练习卷(解析版) 题型:填空题
已知向量a=(-2,3),b∥a,向量b的起点为A(1,2),终点B在坐标轴上,则点B的坐标为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十八第四章第四节练习卷(解析版) 题型:选择题
已知圆O(O为坐标原点)的半径为1,PA,PB为该圆的两条切线,A,B为两切点,那么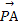 ·
·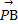 的最小值为( )
的最小值为( )
(A)-4+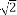 (B)-3+
(B)-3+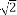
(C)-4+2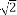 (D)-3+2
(D)-3+2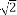
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十九第四章第五节练习卷(解析版) 题型:解答题
已知关于x的方程:x2-(6+i)x+9+ai=0(a∈R)有实数根b.
(1)求实数a,b的值.
(2)若复数满足| -a-bi|-2|z|=0,求z为何值时,|z|有最小值,并求出|z|的最小值.
-a-bi|-2|z|=0,求z为何值时,|z|有最小值,并求出|z|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com