练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知函数f（x）=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}x，x＞0\\{4^x}，x≤0\end{array}$，则f[f（-2）]-16f[f（4）]=（　　）
    A．-3B．3C．-6D．6

    分析 先利用分段函数的性质求出f（-2），f（4），再求出f[f（-2）]，f[f（4）]，由此能求出f[f（-2）]-16f[f（4）]的值．

    解答 解：∵函数f（x）=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}x，x＞0\\{4^x}，x≤0\end{array}$，
    ∴f（-2）=4-2=$\frac{1}{16}$，
    f[f（-2）]=f（$\frac{1}{16}$）=$lo{g}_{\frac{1}{2}}\frac{1}{16}$=4，
    f（4）=$lo{g}_{\frac{1}{2}}4$=-2，
    f[f（4）]=4-2=$\frac{1}{16}$，
    f[f（-2）]-16f[f（4）]=4-16×$\frac{1}{16}$=3．
    故选：B．

    点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意分段函数的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．化简：
    （1）asin0°+bcos90°+ctan180°；
    （2）-p2cos180°+q2sin90°-2pqcos0°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．（1）实数m取什么数值时，复数z=m2-1+（m2-m-2）i分别是：
    ①实数？
    ②虚数？
    ③纯虚数？
    （2）已知$\frac{m}{1+i}$=1-ni，（m、n∈R，i是虚数单位），求m、n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=|x-m|+|x-2|．
    （1）当m=1时，求不等式f（x）≥3的解集；
    （2）若不等式f（x）≥4-x对?x∈R恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若三角形三边分别为AB=7，BC=5，AC=6，则$\overrightarrow{BA}•\overrightarrow{BC}$=（　　）
    A．19B．18C．-18D．-19

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知正数x，y满足x+2y=1，则$\frac{xy}{x+8y}$的最大值为$\frac{1}{18}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．若cos（α+$\frac{π}{2}$）=-$\frac{1}{2}$，α∈（$\frac{π}{2}$，π），则cos（π-α）值为（　　）
    A．$\frac{{\sqrt{3}}}{2}$B．$\frac{1}{2}$C．$-\frac{{\sqrt{3}}}{2}$D．$-\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知f（x）=sin（x+1）$\frac{π}{3}$-$\sqrt{3}$cos（x+1）$\frac{π}{3}$，则f（1）+f（2）+f（3）+…+f（2011）=（　　）
    A．2$\sqrt{3}$B．$\sqrt{3}$C．-$\sqrt{3}$D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

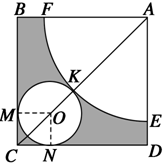    15．如图所示，在边长为$5+\sqrt{2}$的正方形ABCD中，以A为圆心画一个扇形，以O为圆心画一个圆，M，N，K为切点，以扇形为圆锥的侧面，以圆O为圆锥底面，围成一个圆锥，求圆锥的表面积与体积．

    查看答案和解析>>

    同步练习册答案