
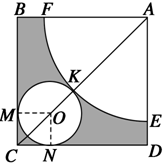
 如图所示,在边长为$5+\sqrt{2}$的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.
如图所示,在边长为$5+\sqrt{2}$的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积. 分析 根据圆的周长等于扇形弧长,以及正方形的对角线列出方程解出圆和扇形的半径,得出圆锥的底面半径,高和母线长.
解答 解:设圆O的半径为r,扇形的半径为R,
则$\left\{\begin{array}{l}{\frac{πR}{2}=2πr}\\{R+r+\sqrt{2}r=(5+\sqrt{2})•\sqrt{2}}\end{array}\right.$,解得R=4$\sqrt{2}$,r=$\sqrt{2}$,
∴围成圆锥的底面半径为$\sqrt{2}$,母线长为l=4$\sqrt{2}$,
∴圆锥的高h=$\sqrt{{l}^{2}-{r}^{2}}$=$\sqrt{30}$.
∴圆锥的表面积S=$π×\sqrt{2}×4\sqrt{2}$+$π×(\sqrt{2})^{2}$=10π.
圆锥的体积V=$\frac{1}{3}×$$π×(\sqrt{2})^{2}×\sqrt{30}$=$\frac{2\sqrt{30}π}{3}$.
点评 本题考查了圆锥的结构特征,面积与体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{5}{2}$] | B. | (-∞,-2] | C. | [-$\frac{5}{2}$,-2] | D. | [-2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com