
分析 连结AC、BD,交于点E,则E是AC中点,取PC中点O,连结OE,推导出O是该四棱锥的外接的球心,可得球半径,由四棱锥的所有顶点都在表面积为16π,建立方程求出PA即可.
解答  解:连结AC,BD交于点E,取PC的中点O,连结OE,则OE∥PA,所以OE⊥底面ABCD,则O到四棱锥的所有顶点的距离相等,即O球心,均为$\frac{1}{2}PC$=$\frac{1}{2}\sqrt{P{A}^{2}+8}$,
解:连结AC,BD交于点E,取PC的中点O,连结OE,则OE∥PA,所以OE⊥底面ABCD,则O到四棱锥的所有顶点的距离相等,即O球心,均为$\frac{1}{2}PC$=$\frac{1}{2}\sqrt{P{A}^{2}+8}$,
所以由球的表面积可得4π($\frac{1}{2}\sqrt{P{A}^{2}+8}$)2=16π,解得PA=$2\sqrt{2}$,
故答案为:$2\sqrt{2}$.
点评 本题考查四面体的外接球的表面积,考查勾股定理的运用,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
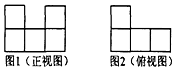 用若干个棱长为1cm的小正方体叠成一个几何体,图1为其正视图,图2为其俯视图,若这个几何体的体积为7cm3,则其侧视图为( )
用若干个棱长为1cm的小正方体叠成一个几何体,图1为其正视图,图2为其俯视图,若这个几何体的体积为7cm3,则其侧视图为( )| A. | 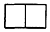 | B. | 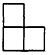 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [1,2) | C. | (1,2] | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com