
分析 给出一个具体函数想研究最值,可以考虑函数的单调性,本题需要对分式型的式子进行变形.
解答 f(x)=$\frac{2016(201{6}^{x}+1)-2}{201{6}^{x}+1}+sinx$=2016+sinx+$\frac{-2}{201{6}^{x}+1}$,
∵0$<a≤\frac{π}{2}$,f(x)在[-a,a]上单调递增,
∴P+Q=f(-a)+f(a)=4032-sina-$\frac{2}{201{6}^{-a}+1}$+sina-$\frac{2}{201{6}^{a}+1}$=4032-$\frac{2×201{6}^{a}}{1+201{6}^{a}}$-$\frac{2}{201{6}^{a}+1}$=4030,
故答案为:4030
点评 本题考查了函数的单调性与最值.对于函数的变形能力及具体函数的单调性的判定有很高的要求


科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (0,1) | C. | (1,+∞) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
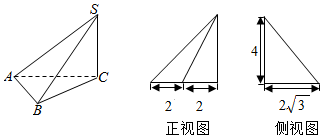 三棱锥S-ABC及其三视图的正视图和俯视图如图所示,则该三棱锥的外接球的表面积是( )
三棱锥S-ABC及其三视图的正视图和俯视图如图所示,则该三棱锥的外接球的表面积是( )| A. | $\frac{112}{3}$π | B. | $\frac{64}{3}$π | C. | 32π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了n名电视观众,如图是观众年龄的频率分布直方图,已知年龄在[30,35)的人数为10人.
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了n名电视观众,如图是观众年龄的频率分布直方图,已知年龄在[30,35)的人数为10人.| 文艺节目 | 新闻节目 | 总计 | |
| 大于或等于20岁至小于40岁 | 40 | ||
| 大于或等于40岁 | 30 | ||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-1,1) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com