练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了n名电视观众，如图是观众年龄的频率分布直方图，已知年龄在[30，35）的人数为10人．
    （Ⅰ）完成下列2×2列联表：
    文艺节目新闻节目总计
    大于或等于20岁至小于40岁40         
    大于或等于40岁   30
    总计
    并据此资料检验，在犯错误的概率不超过0.001的前提下，能否认为收看文艺节目的观众与年龄有关？
    （Ⅱ）根据用分层抽样方法在收看文艺节目的观众中随机抽取6名进一步了解观看节目情况，最后在这6名观众中随机抽出3人获奖，记这获奖3人中年龄大于或等于40岁的人数为ξ，求ξ的分布列与数学期望．
    参考公式与临界值表：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
    P（K2≥k0）0.100.050.0250.0100.0050.001
    k02.7063.8415.0246.6357.87910.828

    分析 （Ⅰ）求出n=100，由图可知大于或等于40岁的观众，可得列联表，代入计算出K2的值，与临界值比较后可得在犯错误的概率不超过0.001的前前下，认为收看文艺节目的观众与年龄有关；
    （Ⅱ）由已知可得ξ的可能值为0、1、2、3，利用综合数计算出随机变量的分布列，代入数学期望公式，可得答案．

    解答 解：（Ⅰ）由图可知$\frac{10}{n}=0.02×5$，所以n=100，又由图可知大于或等于40岁的观众有（0.04+0.03+0.02+0.01）×5×100=50，从而完成2×2列联表如下：

    文艺节目新闻节目总计
    大于或等于20岁小于40岁401050
    大于或等于40岁203050
    总计6040100
    …（3分）
    ∵${K^2}=\frac{{100{{（40×30-20×10）}^2}}}{50×50×60×40}$=$\frac{50}{3}＞16.66＞10.828$…-（5分）
    ∴在犯错误的概率不超过0.001的前前下，认为收看文艺节目的观众与年龄有关…（6分）
    （Ⅱ）用分层抽样方法应抽取20至40岁的观众人数为$\frac{40}{60}×6=4$（名），抽取大于40岁的观众人数为$\frac{20}{60}×6=2$（名）…（7分）
    所以ξ的可能值为0、1、2…（8分）
    $P（ξ=0）=\frac{C_4^3}{C_6^3}=\frac{1}{5}$，$P（ξ=1）=\frac{C_4^2C_2^1}{C_6^3}=\frac{3}{5}$，$P（ξ=2）=\frac{C_4^1C_2^2}{C_6^3}=\frac{1}{5}$，…（10分）
    故ξ的分布列为
    ξ012
    P$\frac{1}{5}$$\frac{3}{5}$$\frac{1}{5}$
    …（11分）
    ξ的数学期望$Eξ=0×\frac{1}{5}+1×\frac{3}{5}+2×\frac{1}{5}=1$…（12分）

    点评 本题考查的知识点是离散型随机变量的期望与方差，分层抽样方法，独立性检验是统计较为综合的题型，难度中档．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    19．已知平面向量$\vec a$，$\vec b$，$\vec e$满足|$\vec e}$|=1，$\vec a$•$\vec e$=2，$\vec b$•$\vec e$=3，|$\vec a$-$\vec b}$|=$\sqrt{5}$，则$\vec a$•$\vec b$的最小值为5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．从一批产品中取出三件产品，设A表示事件“三件产品全不是次品”，B表示事件“三件产品全是次品”，C表示事件“三件产品至少有一件是次品”，则下列结论正确的是（　　）
    A．事件A与C互斥B．任何两个事件均互斥
    C．事件B与C互斥D．任何两个事件均不互斥

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．如图所示，正方体ABCD-A1B1C1D1的棱长为1，E是A1B1上的点，则点E到平面ABC1D1的距离是$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知0＜a≤$\frac{π}{2}$，设函数f（x）=$\frac{{{{2016}^{x+1}}+2014}}{{{{2016}^x}+1}}$+sinx（x∈[-a，a]）的最大值为P，最小值为Q，则P+Q的值为4030．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知a，b，c为△ABC的三个内角A，B，C的对边，向量$\vec m$=（-1，$\sqrt{3}}$），$\vec n$=（cosA，sinA）．若$\vec m$⊥$\vec n$，且acosB+bcosA=csinC，则角A，B的大小分别为（　　）
    A．$\frac{π}{6}$，$\frac{π}{3}$B．$\frac{2π}{3}$，$\frac{π}{6}$C．$\frac{π}{3}$，$\frac{π}{6}$D．$\frac{π}{3}$，$\frac{π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．如图是一个几何体的三视图，则这个几何体的体积为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

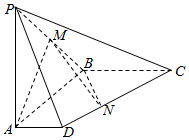    8．如图，在四棱锥P-ABCD中，侧棱PA⊥底面ABCD，AD∥BC，∠ABC=90°，PA=AB=BC=2，AD=1，M是棱PB中点．
    （Ⅰ）求证：平面PBC⊥平面PCD；
    （Ⅱ）设点N是线段CD上一动点，且$\overrightarrow{DN}$=λ$\overrightarrow{DC}$，当直线MN与平面PAB所成的角最大时，求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知命题p：函数f（x）=$\frac{x}{x-1}$的图象的对称中心坐标为（1，1）；命题q：若函数g（x）在区间[a，b]上是增函数，且g（x）＞0，则有g（a）（b-a）＜${∫}_{a}^{b}$g（x）dx＜g（b）（b-a）成立．下列命题为真命题的是（　　）
    A．p∧qB．￢p∧qC．p∧￢qD．￢p∧￢q

    查看答案和解析>>

    同步练习册答案