
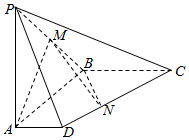
 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.分析 (I)取PC的中点E,连接DE,由四边形ADEM是平行四边形得AM∥DE,由AM⊥平面PBC得DE⊥平面PBC,故而平面PBC⊥平面PCD;
(II)以A为原点建立坐标系,求出$\overrightarrow{MN}$和平面PAB的法向量$\overrightarrow{AD}$,得出|cos<$\overrightarrow{MN},\overrightarrow{AD}$>|关于λ的函数,利用二次函数的性质得出|cos<$\overrightarrow{MN},\overrightarrow{AD}$>|取得最大值时的λ的值.
解答 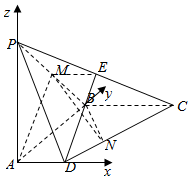 证明:(1)取PC的中点E,则连接DE,
证明:(1)取PC的中点E,则连接DE,
∵ME是△PBC的中位线,
∴ME$\stackrel{∥}{=}\frac{1}{2}BC$,又AD$\stackrel{∥}{=}\frac{1}{2}BC$,
∴ME$\stackrel{∥}{=}$AD,
∴四边形AMED是平行四边形,∴AM∥DE.
∵PA=AB,M是PB的中点,
∴AM⊥PB,
∵PA⊥平面ABCD,BC?平面ABCD,
∴PA⊥BC,又BC⊥AB,PA∩AB=A,
∴BC⊥平面PAB,∵AM?平面PAB,
∴BC⊥AM,
又PB?平面PBC,BC?平面PBC,PB∩BC=B,
∴AM⊥平面PBC,∵AM∥DE,
∴DE⊥平面PBC,又DE?平面PCD,
∴平面PBC⊥平面PCD.
(2)以A为原点,以AD,AB,AP为坐标轴建立空间直角坐标系,如图所示:
则A(0,0,0),B(0,2,0),M(0,1,1),P(0,0,2),C(2,2,0),D(1,0,0).
∴$\overrightarrow{DC}$=(1,2,0),$\overrightarrow{AM}$=(0,1,1),$\overrightarrow{AD}$=(1,0,0),
∴$\overrightarrow{DN}$=λ$\overrightarrow{DC}$=(λ,2λ,0),$\overrightarrow{AN}=\overrightarrow{AD}+\overrightarrow{DN}$=(λ+1,2λ,0),
$\overrightarrow{MN}$=$\overrightarrow{AN}-\overrightarrow{AM}$=(λ+1,2λ-1,-1).
∵AD⊥平面PAB,∴$\overrightarrow{AD}$为平面PAB的一个法向量,
∴cos<$\overrightarrow{AD},\overrightarrow{MN}$>=$\frac{\overrightarrow{AD}•\overrightarrow{MN}}{|\overrightarrow{AD}||\overrightarrow{MN}|}$=$\frac{λ+1}{\sqrt{5{λ}^{2}-2λ+3}}$=$\frac{λ+1}{\sqrt{5(λ+1)^{2}-12(λ+1)+10}}$=$\frac{1}{\sqrt{5-\frac{12}{λ+1}+\frac{10}{(λ+1)^{2}}}}$
=$\frac{1}{\sqrt{10(\frac{1}{λ+1}-\frac{3}{5})^{2}+\frac{7}{5}}}$
设MN与平面PAB所成的角为θ,则sinθ=$\frac{1}{\sqrt{10(\frac{1}{λ+1}-\frac{3}{5})^{2}+\frac{7}{5}}}$.
∴当$\frac{1}{λ+1}=\frac{3}{5}$ 即$λ=\frac{2}{3}$时,sinθ取得最大值,
∴MN与平面PAB所成的角最大时$λ=\frac{2}{3}$.
点评 本题考查了面面垂直的判定,空间向量的应用与线面角的计算,属于中档题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [0,1) | C. | (1,+∞) | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了n名电视观众,如图是观众年龄的频率分布直方图,已知年龄在[30,35)的人数为10人.
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了n名电视观众,如图是观众年龄的频率分布直方图,已知年龄在[30,35)的人数为10人.| 文艺节目 | 新闻节目 | 总计 | |
| 大于或等于20岁至小于40岁 | 40 | ||
| 大于或等于40岁 | 30 | ||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
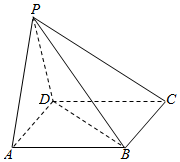 如图,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PA=PD,且PA⊥CD.
如图,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PA=PD,且PA⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com