
分析 根据已知求出m,n的值,进而得到函数的解析式,利用分离常数法,可得函数的值域.
解答 解:由已知中:
1=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{6}$,
1=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{12}$,
1=$\frac{1}{2}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$,
若1=$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{m}$+$\frac{1}{20}$+$\frac{1}{n}$+$\frac{1}{42}$+$\frac{1}{56}$+$\frac{1}{72}$+$\frac{1}{90}$+$\frac{1}{110}$+$\frac{1}{132}$+$\frac{1}{156}$,其中m,n∈N*,且m<n,
∵2=1×2,
6=2×3,
30=5×6,
42=6×7,
56=7×8,
72=8×9,
90=9×10,
110=10×11,
132=11×12,
∴1=$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{m}$+$\frac{1}{20}$+$\frac{1}{n}$+$\frac{1}{42}$+$\frac{1}{56}$+$\frac{1}{72}$+$\frac{1}{90}$+$\frac{1}{110}$+$\frac{1}{132}$+$\frac{1}{156}$=(1-$\frac{1}{4}$)+$\frac{1}{m}$+$\frac{1}{n}$+$\frac{1}{20}$+($\frac{1}{6}$-$\frac{1}{12}$)+$\frac{1}{156}$,
$\frac{1}{m}$+$\frac{1}{n}$=$\frac{m+n}{mn}$=$\frac{43}{390}$,
∴m=13,n=30,
∴函数y=$\frac{(m+n)x}{x-1}$=$\frac{43x}{x-1}$=$\frac{43(x-1)+43}{x-1}$=43+$\frac{43}{x-1}$≠43,
故函数的值域为:{y|y≠43},
故答案为:{y|y≠43}
点评 本题考查的知识点是归纳推理,函数的值域,其中根据已知求出m,n值是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | 事件A与C互斥 | B. | 任何两个事件均互斥 | ||
| C. | 事件B与C互斥 | D. | 任何两个事件均不互斥 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
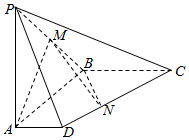 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com