
分析 该题涉及两个变量,故是与面积有关的几何概型,分别表示出满足条件的面积和整个区域的面积,最后利用概率公式解之即可
解答 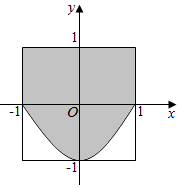 解:由题意可得,在区间[-1,1]内随机取两个实数x,y,对应的区域是边长为2的正方形,如图,面积为4,
解:由题意可得,在区间[-1,1]内随机取两个实数x,y,对应的区域是边长为2的正方形,如图,面积为4,
满足y≥x2-1的区域为图中阴影部分,面积为2+${∫}_{-1}^{1}(1-{x}^{2})dx$=2+(x-$\frac{1}{3}{x}^{3}$)|${\;}_{-1}^{1}$=$\frac{10}{3}$
∴满足y≥x2-1的概率是$\frac{\frac{10}{3}}{4}=\frac{5}{6}$.
故答案为:$\frac{5}{6}$;
点评 本题主要考查了与面积有关的几何概率的求解,解题的关键是准确求出区域的面积,属于中档题.


科目:高中数学 来源: 题型:解答题
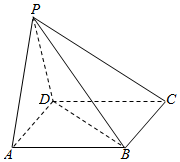 如图,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PA=PD,且PA⊥CD.
如图,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PA=PD,且PA⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆$\frac{{y}^{2}}{36}$+$\frac{{x}^{2}}{18}$=1上的一点,从原点O向圆R(x-x0)2+(y-y0)2=12作两条切线,分别交椭圆于P,Q两点.
如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆$\frac{{y}^{2}}{36}$+$\frac{{x}^{2}}{18}$=1上的一点,从原点O向圆R(x-x0)2+(y-y0)2=12作两条切线,分别交椭圆于P,Q两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com