
分析 (Ⅰ)运用公式法解绝对值不等式;(Ⅱ)分别对有关y的式子和x的式子求最值.
解答 解:(Ⅰ)解不等式|2x|≤2m-1,所以$\frac{1}{2}-m≤x≤m-\frac{1}{2}$,则m-$\frac{1}{2}$=2,m=$\frac{5}{2}$
(Ⅱ)|2x-1|-|2x+3|$≤{2}^{y}+\frac{a}{{2}^{y}}$对任意y∈R恒成立,而${2}^{y}+\frac{a}{{2}^{y}}≥2\sqrt{a}$,所以2$\sqrt{a}$≥|2x-1|-|2x-3|,则$\sqrt{a}≥|x-\frac{1}{2}|-|x+\frac{3}{2}|$,而$|x-\frac{1}{2}|-|x+\frac{3}{2}|≤|(x-\frac{1}{2})-(x+\frac{3}{2})|=2$
∴a≥4,a的最小值为4.
点评 本题第一问考查了绝对值不等式的解法.第二问考查了双变元的恒成立问题.要求学生熟练掌握绝对值三角不等式.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
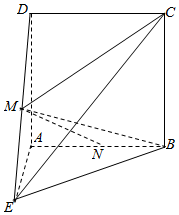 如图,正方形ABCD所在平面与直角三角形ABE所在的平面相互垂直,AE⊥AB,设M,N分别是DE,AB的中点,已知AB=2,AE=1.
如图,正方形ABCD所在平面与直角三角形ABE所在的平面相互垂直,AE⊥AB,设M,N分别是DE,AB的中点,已知AB=2,AE=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$,$\frac{π}{3}$ | B. | $\frac{2π}{3}$,$\frac{π}{6}$ | C. | $\frac{π}{3}$,$\frac{π}{6}$ | D. | $\frac{π}{3}$,$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
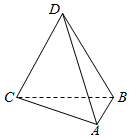 已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在的平面互相垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的体积为( )
已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在的平面互相垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的体积为( )| A. | $\frac{4π}{3}$ | B. | $\frac{{4\sqrt{3}π}}{3}$ | C. | $\frac{32π}{3}$ | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
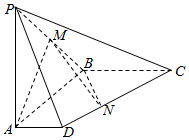 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [-1,2) | C. | [-1,+∞) | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com