Question

9．已知命题p：函数f（x）=$\frac{x}{x-1}$的图象的对称中心坐标为（1，1）；命题q：若函数g（x）在区间[a，b]上是增函数，且g（x）＞0，则有g（a）（b-a）＜${∫}_{a}^{b}$g（x）dx＜g（b）（b-a）成立．下列命题为真命题的是（　　）

• A． p∧q
• B． ￢p∧q
• C． p∧￢q
• D． ￢p∧￢q

Answer 1

分析 变形即可判断命题p的真假，利用定积分的性质即可判断出q的真假，根据复合命题真假关系进行的判断．

解答 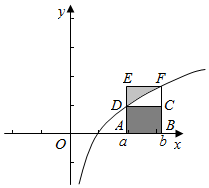解：f（x）=$\frac{x}{x-1}$=$\frac{x-1+1}{x-1}$=1+$\frac{1}{x-1}$，则函数f（x）的图象的对称中心坐标为（1，1）；故p是真命题，
若函数g（x）在区间[a，b]上是增函数，若a＜x＜b，则g（a）＜g（x）＜g（b），
则有积分的应用可知定义面积满足，
S_矩形ABCD＜S_曲边ABFD＜S_矩形ABFE，
∴g（a）（b-a）＜${∫}_{a}^{b}$g（x）dx＜g（b）（b-a），因此成立，即是真命题．
则p∧q是真命题．
故选：A

点评 本题主要考查命题的真假判断，根据分式函数的性质以及积分的应用判断命题p，q的真假是解决本题的关键．