
分析 利用圆心到直线的距离小于等于半径可得到直线与圆有公共点,可求出满足条件的k,最后根据几何概型的概率公式可求出所求
解答 解:圆x2+y2=r2的圆心为(0,0),
圆心到直线x+y+2=0的距离为$\frac{2}{\sqrt{2}}=\sqrt{2}$,
要使圆x2+y2=r2与直线x+y+2=0存在公共点,
则$\sqrt{2}≤$r,
∴在区间[1,2]上随机取一个数r,使圆x2+y2=r2与直线x+y+2=0存在公共点的概率为$\frac{2-\sqrt{2}}{2-1}=2-\sqrt{2}$;
故答案为:$2-\sqrt{2}$.
点评 本题主要考查了几何概型的概率,以及直线与圆相交的性质,解题的关键弄清概率类型,同时考查了计算能力.


科目:高中数学 来源: 题型:解答题
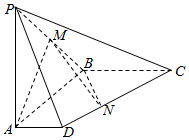 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{65}{56}$ | B. | $\frac{65}{56}$ | C. | $\frac{7}{8}$ | D. | $\frac{9}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
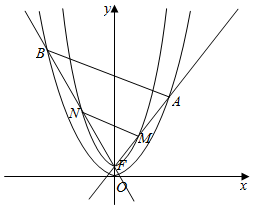 抛物线C1:x2=2py(p>0)的焦点F是C2:y=$\frac{1}{2}$x2+1的顶点,过F点的直线l1,l2的斜率分别是k1,k2,且k1•k2=-2,直线l1与C1,C2交于A,C,M,直线l2与C1,C2交于B,D,N
抛物线C1:x2=2py(p>0)的焦点F是C2:y=$\frac{1}{2}$x2+1的顶点,过F点的直线l1,l2的斜率分别是k1,k2,且k1•k2=-2,直线l1与C1,C2交于A,C,M,直线l2与C1,C2交于B,D,N查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com