
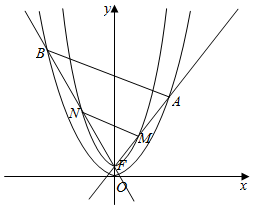
 抛物线C1:x2=2py(p>0)的焦点F是C2:y=$\frac{1}{2}$x2+1的顶点,过F点的直线l1,l2的斜率分别是k1,k2,且k1•k2=-2,直线l1与C1,C2交于A,C,M,直线l2与C1,C2交于B,D,N
抛物线C1:x2=2py(p>0)的焦点F是C2:y=$\frac{1}{2}$x2+1的顶点,过F点的直线l1,l2的斜率分别是k1,k2,且k1•k2=-2,直线l1与C1,C2交于A,C,M,直线l2与C1,C2交于B,D,N分析 (Ⅰ)求出C2:y=$\frac{1}{2}$x2+1的顶点,可得抛物线C1:x2=2py(p>0)的焦点,即可求抛物线C1的方程;求出直线MN的方程,即可证明直线MN过定点.
(Ⅱ)①表示出△MFN面积,利用基本不等式,即可求△MFN面积的最小值;
②分别求出△ABF,△MNF,△CDF的面积,即可证明S22=4S1•S3.
解答 (Ⅰ)证明:${C_2}:y=\frac{1}{2}{x^2}+1$的顶点F(0,1),抛物线C1:x2=4y--------------(2分)
直线l1:y=k1x+1,l2:y=k2x+1
$\left\{{\begin{array}{l}{y={k_1}x+1}\\{{x^2}=4y}\end{array}}\right.⇒{x^2}-4{k_1}x-4=0$,
设A(x1,y1),C(x2,y2)x1+x2=4k1,x1x2=-4--------------------------------------①----------------------(3分)
${x_M}=\frac{{{x_1}+{x_2}}}{2}=2{k_1},{y_M}=2k_1^2+1,即M({2{k_1},2k_1^2+1})$,
同理$N({2{k_2},2k_2^2+1})$,
M,N两点的坐标满足方程${C_2}:y=\frac{1}{2}{x^2}+1$,--------------------------------(5分)
${k_{MN}}=\frac{{2({k_2^2-k_1^2})}}{{2{k_2}-2{k_1}}}={k_2}+{k_1}$
直线$MN:y-2k_1^2-1=({{k_1}+{k_2}})(x-2{k_1})=({{k_1}+{k_2}})x-2k_1^2-2{k_1}{k_2}$
∵${k_1}{k_2}=-2∴y-2k_1^2-1=({{k_1}+{k_2}})x-2k_1^2-2{k_1}{k_2}$
即y=(k1+k2)x+5,
所以直线MN过定点(0,5)----------------------------(7分)
(II)①解:$|MN|=\sqrt{{{({2{k_1}-2{k_2}})}^2}+{{({2k_1^2-2k_2^2})}^2}}=2\sqrt{{{({{k_1}-{k_2}})}^2}[{1+{{({{k_1}+{k_2}})}^2}}]}$
F到直线MN的距离$d=\frac{4}{{\sqrt{1+{{({{x_1}+{x_2}})}^2}}}}$--------------------------------(8分)
${S_{△FMN}}=\frac{1}{2}|MN|×d=4\sqrt{{{({{k_1}-{k_2}})}^2}}=4\sqrt{k_1^2+k_2^2-2{k_1}{k_2}}$
=$4\sqrt{k_1^2+k_2^2+4}≥4\sqrt{2|{k_1}||{k_2}|+4}=4\sqrt{8}=8\sqrt{2}$-------------------(10分)
②证明:设A(x1,y1),C(x2,y2),B(x3,y3),D(x4,y4)
x1+x2=4k1,x1x2=-4,x3+x4=2k2,x3x4=-4,
${y_1}{y_2}=\frac{1}{16}x_1^2x_2^2=1,{y_1}+{y_2}={k_1}({{x_1}+{x_2}})+2=4k_1^2+2$,${y_3}{y_4}=1,{y_3}+{y_4}=4k_2^2+2$$∠AFB=θ,{S_1}{S_3}=\frac{1}{2}|FA||FB|sinθ×\frac{1}{2}|FC||FD|sinθ$=$\frac{1}{4}({{y_1}+1})({{y_2}+1})({{y_3}+1})({{y_4}+1}){sin^2}θ$
=$\frac{1}{4}({{y_1}{y_2}+{y_1}+{y_2}+1})({{y_3}{y_4}+{y_3}+{y_4}+1}){sin^2}θ$
=$\frac{1}{4}({4k_1^2+4})({4k_2^2+4}){sin^2}θ=4({k_1^2+1})({k_2^2+1}){sin^2}θ$-------------(12分)
$S_2^2=\frac{1}{4}|FM{|^2}|FN{|^2}{sin^2}θ=\frac{1}{4}({4k_1^2+4k_1^4})({4k_2^2+4k_2^4}){sin^2}θ$
=$4k_1^2k_2^2({1+k_1^2})({1+k_2^2}){sin^2}θ=16({1+k_1^2})({1+k_2^2}){sin^2}θ$
所以$S_2^2=4{S_1}{S_3}$------------------------------(14分)
点评 本题考查直线与圆锥曲线的综合题,考查了根与系数的关系,三角形的面积公式,抛物线的性质等,解题的关键是认真审题准确转化题设中的关系,本题综合性强,符号计算运算量大,解题时要认真严谨避免马虎出错.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 24 | C. | 64 | D. | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com