
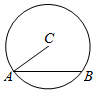
 如图所示,圆C中,弦AB的长度为4,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为8.
如图所示,圆C中,弦AB的长度为4,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为8. 分析 根据向量数量积的定义和公式转化为投影的关系进行求解即可.
解答  解:取AB的中点D,则AD是向量$\overrightarrow{AC}$在$\overrightarrow{AB}$上的投影,
解:取AB的中点D,则AD是向量$\overrightarrow{AC}$在$\overrightarrow{AB}$上的投影,
则$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos<$\overrightarrow{AB}$,$\overrightarrow{AC}$>=|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|=4×2=8,
故答案为:8
点评 本题主要考查向量数量积的应用,根据向量数量积的公式结合向量投影的定义进行转化是解决本题的关键.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:解答题
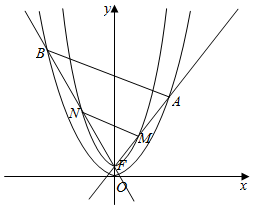 抛物线C1:x2=2py(p>0)的焦点F是C2:y=$\frac{1}{2}$x2+1的顶点,过F点的直线l1,l2的斜率分别是k1,k2,且k1•k2=-2,直线l1与C1,C2交于A,C,M,直线l2与C1,C2交于B,D,N
抛物线C1:x2=2py(p>0)的焦点F是C2:y=$\frac{1}{2}$x2+1的顶点,过F点的直线l1,l2的斜率分别是k1,k2,且k1•k2=-2,直线l1与C1,C2交于A,C,M,直线l2与C1,C2交于B,D,N查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p∧q为假命题,则p、q均为假命题 | |
| B. | 函数f(x)=x2-x-6的零点是(3,0)或(-2,0) | |
| C. | 对于命题p:?x∈R,使得x2-x-6>0,则¬p:?x∈R,均有x2-x-6≤0 | |
| D. | 命题“若x2-x-6=0,则x=3”的否命题为“若x2-x-6=0,则x≠3” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com