
【题目】如图,三棱柱![]() 的棱长均为2,O为AC的中点,平面A'OB⊥平面ABC,平面
的棱长均为2,O为AC的中点,平面A'OB⊥平面ABC,平面![]() ⊥平面ABC.
⊥平面ABC.
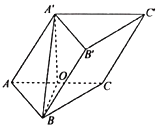
(1)求证:A'O⊥平面ABC;
(2)求二面角A﹣BC﹣C'的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由已知可得AC⊥BO,平面A'OB⊥平面ABC,可证AC⊥平面BOA′,进而证明AC⊥A′O,再由面![]() ⊥平面ABC.,即可证明结论;
⊥平面ABC.,即可证明结论;
(2)以O为原点建立空间直角坐标系,求出![]() 坐标,求出平面
坐标,求出平面![]() 法向量坐标,取平面ABC的法向量为
法向量坐标,取平面ABC的法向量为![]() (0,0,1),根据空间向量面面角公式,即可求解.
(0,0,1),根据空间向量面面角公式,即可求解.
(1)证明:∵三棱柱ABC﹣A'B'C'的棱长均为2,
O为AC的中点,∴AC⊥BO,
∵平面A'OB⊥平面ABC,平面A'OB∩平面ABC=OB,
![]() 平面ABC,∴AC⊥平面BOA′,
平面ABC,∴AC⊥平面BOA′,
![]() 平面BOA′,∴AC⊥A′O,
平面BOA′,∴AC⊥A′O,
∵平面AA'C'C⊥平面ABC,平面AA'C'C∩平面ABC=AC.
![]() 平面
平面![]() ,∴A'O⊥平面ABC.
,∴A'O⊥平面ABC.
(2)解:由(1)得A'O⊥平面ABC,因为![]() 平面ABC,所以A'O⊥
平面ABC,所以A'O⊥![]() .
.
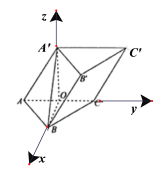
以O为原点,OB为x轴,OC为y轴,OA′为z轴,
建立空间直角坐标系,则A(0,﹣1,0),B(![]() ,0,0),
,0,0),
C(0,1,0),C′(0,2,![]() ),
),
![]() (
(![]() ,1,0),
,1,0),![]() (
(![]() ,2,
,2,![]() ),
),
设平面BCC′的法向量![]() (x,y,z),
(x,y,z),
则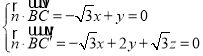 ,
,
取x=1,则![]() ,得
,得![]() (1,
(1,![]() ,﹣1),
,﹣1),
平面ABC的法向量![]() (0,0,1),
(0,0,1),
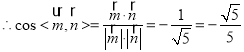 .
.
∴二面角A﹣BC﹣C'的余弦值为![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() +
+![]() =1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2
=1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过右焦点F2的直线l交椭圆于A,B两点,若y轴上一点M(0,![]() )满足|MA|=|MB|,求直线l的斜率k的值.
)满足|MA|=|MB|,求直线l的斜率k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其右焦点
,其右焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() 是
是![]() 与椭圆
与椭圆![]() 的两个交点,
的两个交点,![]() 是
是![]() 与椭圆
与椭圆![]() 的两个交点,
的两个交点,![]() 分别是线段
分别是线段![]() 的中点,试判断直线
的中点,试判断直线![]() 是否过定点?若过定点,求出该定点的坐标;若不过定点.请说明理由.
是否过定点?若过定点,求出该定点的坐标;若不过定点.请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程是
的参数方程是 (m>0,t为参数),曲线
(m>0,t为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB中点,PC=3PE.
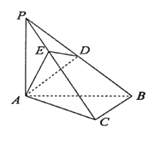
(1)求证:平面ADE⊥平面PBC;
(2)在AC上是否存在一点M,使得MB∥平面ADE?若存在,请确定点M的位置,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,命题p:“x∈[1,2],x2﹣a≥0”,命题q:“x∈R,x2+2ax+2﹣a=0”.
(1)若命题p为真命题,求实数a的取值范围;
(2)若命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com