
 已知长方体ABCD-A'B'C'D'中,AB=4,AD=3,AA'=2;
已知长方体ABCD-A'B'C'D'中,AB=4,AD=3,AA'=2;分析 (1)建立空间直角坐标系,求出两条线段的方向向量,代入向量夹角公式,可得答案.
(2)连接BD',DB'交于点O,则点O即为AC'与平面D'DBB'的交点,根据长方体的性质,可得结论.
解答 解:(1)建立如图所示空间直角坐标系,
∵AB=4,AD=3,AA'=2;
∴C'(4,3,2),B(4,0,0),D(0,3,0)
则:$\overrightarrow{{AC′}^{\;}}$=(4,3,2),$\overrightarrow{BD}$=(-4,3,0)
异面直线AC'和BD所成角的余弦值为:$\frac{|\overrightarrow{{AC′}^{\;}}•\overrightarrow{BD}|}{\left|\overrightarrow{{AC′}^{\;}}\right|•\left|\overrightarrow{BD}\right|}$=$\frac{7}{\sqrt{29}•5}$=$\frac{7\sqrt{29}}{145}$;
(2)连接BD',DB'交于点O,则点O即为AC'与平面D'DBB'的交点,
根据长方体的几何特征可得:
O为长方体ABCD-A'B'C'D'外接球的球心,
AC'为长方体ABCD-A'B'C'D'外接球的直径,
故O为AC'中点,
又由BD',DB'交于点O,故O在平面D'DBB'上,
故O即为AC'与平面D'DBB'的交点.
点评 本题考查的知识点是空间直线与直线,直线与平面的位置关系,异面直线的夹角,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
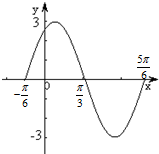 已知函数y=Asin(ωx+φ)(A>0,ω>0)|φ|<$\frac{π}{2}$的图象如图所示,
已知函数y=Asin(ωx+φ)(A>0,ω>0)|φ|<$\frac{π}{2}$的图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{24}$ | B. | x=$\frac{5π}{12}$ | C. | x=$\frac{π}{2}$ | D. | x=$\frac{π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com