
【题目】
已知函数![]() =(sin x+cos x)2+cos 2x.
=(sin x+cos x)2+cos 2x.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)![]() (2)f(x)在
(2)f(x)在![]() 上的最大值为
上的最大值为![]() +1,最小值为0.
+1,最小值为0.
【解析】试题分析: ![]() 根据二倍角公式和两角和的正弦公式对
根据二倍角公式和两角和的正弦公式对![]() 化简,得到
化简,得到![]() 的形式,利用最小正周期计算公式即可求解;
的形式,利用最小正周期计算公式即可求解;
![]() 根据定义域求出
根据定义域求出![]() 的取值范围,进而得到
的取值范围,进而得到![]() 的取值范围,从而得到函数
的取值范围,从而得到函数![]() 的最值。
的最值。
解析:(1)因为f(x)=sin2x+cos2x+2sin xcos x+cos 2x=1+sin 2x+cos 2x=![]() sin
sin![]() +1,
+1,
所以函数f(x)的最小正周期T=![]() =π.
=π.
(2)由(1)知,f(x)=![]() sin
sin![]() +1.
+1.
当x∈![]() 时,2x+
时,2x+![]() ∈
∈![]() ,
,
由正弦函数y=sin x在![]() 上的图象知,
上的图象知,
当2x+![]() =
=![]() ,即x=
,即x=![]() 时,f(x)取最大值
时,f(x)取最大值![]() +1;
+1;
当2x+![]() =
=![]() ,即x=
,即x=![]() 时,f(x)取最小值0.
时,f(x)取最小值0.
综上,f(x)在![]() 上的最大值为
上的最大值为![]() +1,最小值为0.
+1,最小值为0.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的焦点在
的焦点在 ![]() 轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(1)当t=4, ![]() 时,求△AMN的面积;
时,求△AMN的面积;
(2)当 ![]() 时,求k的取值范围.
时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P﹣A1B1C1D1 , 下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
(1)若AB=6m,PO1=2m,则仓库的容积是多少?
(2)若正四棱柱的侧棱长为6m,则当PO1为多少时,仓库的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+![]() }是等比数列.
}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56
B.60
C.120
D.140
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列等式:
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2=
)﹣2= ![]() ×1×2;
×1×2;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+sin(
)﹣2+sin( ![]() )﹣2=
)﹣2= ![]() ×2×3;
×2×3;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+sin(
)﹣2+…+sin( ![]() )﹣2=
)﹣2= ![]() ×3×4;
×3×4;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+sin(
)﹣2+…+sin( ![]() )﹣2=
)﹣2= ![]() ×4×5;
×4×5;
…
照此规律,
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+(sin
)﹣2+…+(sin ![]() )﹣2= .
)﹣2= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1 .
(1)求数列{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面斜坐标系xOy中,∠xOy=60°,平面上任意一点P关于斜坐标系的斜坐标是这样定义的:若![]() =xe1+ye2(其中e1,e2分别为x轴、y轴同方向的单位向量),则点P的斜坐标为(x,y).
=xe1+ye2(其中e1,e2分别为x轴、y轴同方向的单位向量),则点P的斜坐标为(x,y).
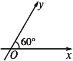
(1)若点P在斜坐标系xOy中的斜坐标为(2,-2),求点P到原点O的距离.
(2)求以原点O为圆心,1为半径的圆在斜坐标系xOy中的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com