
 如图,ABCD为正方形,P为平面ABCD外一点,且PA⊥平面ABCD,则关于平面PAB、平面PBC、平面PAD的位置关系下列说法正确的有①④⑤
如图,ABCD为正方形,P为平面ABCD外一点,且PA⊥平面ABCD,则关于平面PAB、平面PBC、平面PAD的位置关系下列说法正确的有①④⑤分析 由P是正方形ABCD外一点,且PA⊥平面ABCD,知AB⊥BC,PA⊥BC,故BC⊥面PAB,所以平面PAB⊥平面PBC;由P是正方形ABCD外一点,且PA⊥平面ABCD,知AD⊥AB,PA⊥AD,故AD⊥面PAB,所以平面PAB⊥平面PAD.
解答 解:由于BC⊥AB,由PA垂直于正方形ABCD所在平面,所以BC⊥PA,
易证BC⊥平面PAB,则平面PAB⊥平面PBC;又AD∥BC,故AD⊥平面PAB,
则平面PAD⊥平面PAB.①对③不对
平面PBC与平面PAD相交但不垂直,④对②不对;
若平面PBC与平面PAD的交线为l,与AD平行,故l⊥面PAB,即⑤正确.
故答案为:①④⑤.
点评 本题考查面面垂直的判定定理的应用,要注意转化思想的应用,将面面垂直转化为线面垂直.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的正方体ABCD-A1B1C1D1中,
在如图所示的正方体ABCD-A1B1C1D1中,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
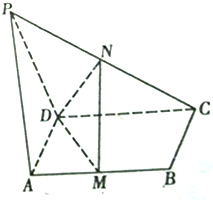 如图,已知PA⊥平面ABCD,ABCD为矩形,M、N为AB、PC的中点.
如图,已知PA⊥平面ABCD,ABCD为矩形,M、N为AB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com