
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| . |
| A |
| . |
| A |
| . |
| A |
| . |
| A |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 12 |
|
| . |
| A |
| . |
| B |
| . |
| A |
| . |
| B |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 12 |
| ξ | 2 | 3 | 4 | ||||||
| P |
|
|
|


科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示更换的面数,用
表示更换的面数,用 表示更换费用。
表示更换费用。 的分布列,求
的分布列,求 的数学期望。
的数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为随机变量,求
为随机变量,求 的分布列。
的分布列。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,转盘(B)指针所对的区域为
,转盘(B)指针所对的区域为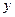 ,
, 、
、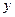

 ,设
,设 +
+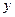 的值为
的值为 ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为 .
.  <2且
<2且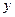 >1的概率;
>1的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com