
 ,转盘(B)指针所对的区域为
,转盘(B)指针所对的区域为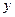 ,
, 、
、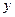

 ,设
,设 +
+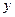 的值为
的值为 ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为 .
.  <2且
<2且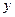 >1的概率;
>1的概率;科目:高中数学 来源:不详 题型:解答题
 校高三年级学生家庭月平均收入不多于10000元的共有100
校高三年级学生家庭月平均收入不多于10000元的共有100 0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.
0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.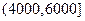 (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在 (元)间的同学不发助学金.
(元)间的同学不发助学金.
 元,写出
元,写出 的分布列,并计算该企业发放该年级的助学金约需要的资金;
的分布列,并计算该企业发放该年级的助学金约需要的资金; 元,求
元,求 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.
| B.
| ||||||||||||||||||||||||||||
C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com