
分析 求得椭圆的a=6,运用椭圆的定义可得|AF1|+|AF2|=2a=12,由向量的中点表示形式,可得B为AF1的中点,C为AF2的中点,运用中位线定理和椭圆定义,即可得到所求值.
解答 解:椭圆$\frac{x^2}{36}+\frac{y^2}{27}$=1的a=6,
由椭圆的定义可得|AF1|+|AF2|=2a=12,
$\overrightarrow{OB}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{{OF}_{1}}$),可得B为AF1的中点,
$\overrightarrow{OC}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{O{F}_{2}}$),可得C为AF2的中点,
由中位线定理可得|OB|=$\frac{1}{2}$|AF2|,
|OC|=$\frac{1}{2}$|AF1|,
即有|$\overrightarrow{OB}$|+|$\overrightarrow{OC}$|=$\frac{1}{2}$(|AF1|+|AF2|)=a=6,
故答案为:6.
点评 本题考查椭圆的定义、方程和性质,考查向量的中点表示形式,同时考查中位线定理,运用椭圆的第一定义是解题的关键,属于中档题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
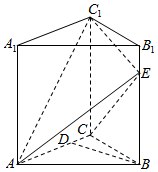 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=2$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上一点,BD∥平面AC1E.
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=2$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上一点,BD∥平面AC1E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{3}{2}$i | C. | -$\frac{3}{2}$i | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 5 | C. | 2$\sqrt{5}$ | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | 100 | 160 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com