
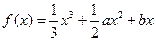
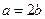 ,试问函数
,试问函数 能否在
能否在 取到极值?若有可能,求出实数
取到极值?若有可能,求出实数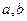 的值;否则说明理由.
的值;否则说明理由. 在区间(-1,2),(2,3)内各有一个极值点,试求
在区间(-1,2),(2,3)内各有一个极值点,试求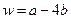 的取值范围.
的取值范围. 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
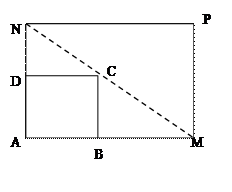 (Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 km处的海岸渔站中,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸可以使抵达渔站的时间最省?
km处的海岸渔站中,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸可以使抵达渔站的时间最省?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润
型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润 确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管
确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管 型电脑出厂价仅是1993年出厂价的
型电脑出厂价仅是1993年出厂价的 ,但却实现了
,但却实现了 纯利润的高效益.
纯利润的高效益. 型电脑的生产成本;
型电脑的生产成本; ,以下数据可供参考:
,以下数据可供参考: ,
, ).
).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com