
已知函数 .
.
(1)若存在 ,使不等式
,使不等式 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(2)设 ,证明:
,证明: .
.
(1)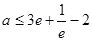 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)这是一个含参不等式恒成立,求参数取值范围的问题,通常方法是根据函数性质进行求解,或分离参数转化为求函数最值问题,若方便分离参数又较容易求分离后函数的最值,还是分离参数较好,这样可避免对参数的讨论;(2)这是一个以函数的凹凸那条性为背景的一个不等式的证明问题双变元问题,可以将其中一个看成主元,另一个看成参数,构造函数 ,通过求导判断函数的单调性和最值达到证明的目的.
,通过求导判断函数的单调性和最值达到证明的目的.
试题解析:(1)(1)由 变形为
变形为 .
.
令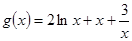 ,则
,则
故当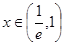 时,
时, ,
, 在
在 上单调递减;
上单调递减;
当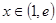 时,
时, ,
, 在
在 上单调递增,
上单调递增,
所以 的最大值只能在
的最大值只能在 或
或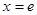 处取得
处取得
又 ,
,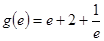 ,所以
,所以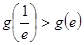
所以 ,从而
,从而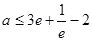 .
.
(2)∵ ,∴
,∴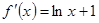
设 ,则
,则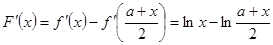
当 时,
时, ,
,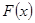 在
在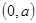 上为减函数;
上为减函数;
当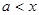 时,
时, ,
,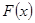 在
在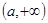 上为增函数.
上为增函数.
从而当 时,
时,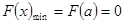 ,
,
因为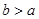 ,所以
,所以 .
.
考点:函数的零点、三角函数的性质.


科目:高中数学 来源: 题型:解答题
已知函数 ,
, .
.
(1)若 ,是否存在
,是否存在 、
、 ,使
,使 为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;
为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;
(2)若 ,
, ,求
,求 在
在 上的单调区间;
上的单调区间;
(3)已知 ,
, 对
对 ,,有
,,有 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, 恒过定点 (3,2).
恒过定点 (3,2).
(1)求实数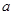 ;
;
(2)在(1)的条件下,将函数 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移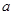 个单位后得到函数
个单位后得到函数 ,设函数
,设函数 的反函数为
的反函数为 ,求
,求 的解析式;
的解析式;
(3)对于定义在[1,9]的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: .已知甲、乙两地相距100千米.
.已知甲、乙两地相距100千米.
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(Ⅰ)已知二次函数 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(Ⅱ)若 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;
(Ⅲ)若 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com