
【题目】已知数列{![]() }的首项a1=2,前n项和为
}的首项a1=2,前n项和为![]() ,且数列{
,且数列{![]() }是以
}是以![]() 为公差的等差数列·
为公差的等差数列·
(1)求数列{![]() }的通项公式;
}的通项公式;
(2)设![]() ,
,![]() ,数列{
,数列{![]() }的前n项和为
}的前n项和为![]() ,
,
①求证:数列{![]() }为等比数列,
}为等比数列,
②若存在整数m,n(m>n>1),使得![]() ,其中
,其中![]() 为常数,且
为常数,且![]() -2,求
-2,求![]() 的所有可能值.
的所有可能值.
【答案】(1)![]() ;(2)①见证明;②当n=2,m=4时,λ=-2,当n=2,m=3时,λ=-1.
;(2)①见证明;②当n=2,m=4时,λ=-2,当n=2,m=3时,λ=-1.
【解析】
(1)先求解等差数列![]() 的通项公式,再根据
的通项公式,再根据![]() 求解
求解![]() 的通项公式;(2)①采用错位相减法先求
的通项公式;(2)①采用错位相减法先求![]() ,再根据
,再根据 ,证明
,证明![]() 为等比数列;②将所给的等式变形,然后得到对应的等量关系,接着分析此等量关系(借助数列的单调性)在什么时候满足即
为等比数列;②将所给的等式变形,然后得到对应的等量关系,接着分析此等量关系(借助数列的单调性)在什么时候满足即![]() 取什么值时能满足要求.
取什么值时能满足要求.
(1)因为![]() ,所以
,所以![]()
所以![]()
即![]()
当![]() 时,
时,![]()
∴![]()
当n=1时,![]() ,符合上述通项,所以
,符合上述通项,所以![]()
(2)①因为![]() ,所以
,所以![]()
所以![]()
则![]()
两式相减,可整理得![]()
∴![]() ,
,![]() ,且
,且![]()
所以数列![]() 是以4为首项,2为公比的等比数列.
是以4为首项,2为公比的等比数列.
②由①可知,![]() ,且由(1)知
,且由(1)知![]() ,代入
,代入![]()
可得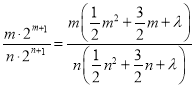
整理得![]()
即:![]() ,设
,设![]() ,则
,则![]()
则![]()
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]()
因为![]() ,且
,且![]()
所以![]()
所以![]() 或
或![]() ,即n=2,m=4或3
,即n=2,m=4或3
当n=2,m=4时,λ=-2,
当n=2,m=3时,λ=-1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() .
.
(1)求C的方程;
(2)若直线l与C有且只有一个公共点,l与圆x2+y2=6交于A,B两点,直线OA,OB的斜率分别记为k1,k2.试判断k1k2是否为定值,若是,求出该定值;否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
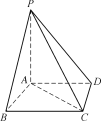
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的有( )
①用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
②若一组数据8,12,x,11,9的平均数是10,则其方差是2;
③回归直线一定过样本点的中心(![]() );
);
④若相关系数![]() ,则两个变量之间线性关系性强.
,则两个变量之间线性关系性强.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别为椭圆的右顶点、上顶点和右焦点,且
分别为椭圆的右顶点、上顶点和右焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() :
: ![]() 被圆
被圆![]() :
: ![]() 所截得的弦长为
所截得的弦长为![]() ,若直线
,若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥于2018年10月2刻日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55千米.桥面为双向六车道高速公路,大桥通行限速100km/h,现对大桥某路段上1000辆汽车的行驶速度进行抽样调查.画出频率分布直方图(如图),根据直方图估计在此路段上汽车行驶速度在区间[85,90)的车辆数和行驶速度超过90km/h的频率分别为( )
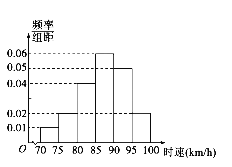
A. 300,![]() B. 300,
B. 300,![]() C. 60,
C. 60,![]() D. 60,
D. 60,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com