练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知变量x，y满足约束条件$\left\{\begin{array}{l}{x-4y+3≥0}\\{x+y≥0}\\{x≥1}\end{array}\right.$，目标函数z=2x+y，则（　　）
    A．z的最小值为3，z无最大值B．z的最小值为1，最大值为3
    C．z的最小值为3，z无最小值D．z的最小值为1，z无最大值

    分析 由约束条件作出可行域，数形结合得到最优解，求出最优解的坐标，代入目标函数得答案．

    解答 解：由约束条件作出可行域如图，
    化目标函数z=2x+y为y=-2x+z，
    由图可知，当直线y=-2x+z过A（1，-1）时
    直线在y轴上的截距最小，z最小，为2×1-1=1，
    无最大值．
    故选：D．

    点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届湖南衡阳县四中高三9月月考数学（文）试卷（解析版） 题型：选择题

    具有性质：的函数，我们称为满足“倒负”变换的函数，下列函数：

    ①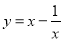；②；③其中满足“倒负”变换的函数是（ ）

    A．①② B．①③ C．②③ D．①

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．将函数f（x）=$\sqrt{2}$sin2x-$\sqrt{2}$cos2x+1的图象向左平移$\frac{π}{4}$个单位，再向下平移1个单位，得到函数y=g（x）的图象，则下列关予函数y=g（x）的说法错误的是（　　）
    A．函数y=g（x）的最小正周期为π
    B．函数y=g（x）的图象的一条对称轴为直线x=$\frac{π}{8}$
    C．${∫}_{0}^{\frac{π}{2}}$g（x）dx=$\sqrt{2}$
    D．函数y=g（x）在区间[$\frac{π}{12}$，$\frac{5π}{8}$]上单调递减

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知g（x）=mx+2，f（x）=x2-2x，若对?x1∈[-1，2]．?x0∈[-1，2]，有g（x1）=f（x0）成立，则m的取值范围是[-1，$\frac{1}{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．设a＞0，若关于x，y的不等式组$\left\{\begin{array}{l}{ax-y+2≥0}\\{x+y-2≥0}\\{x-2≤0}\end{array}\right.$，表示的可行域与圆（x-2）2+y2=9存在公共点，则z=x+2y的最大值的取值范围为（　　）
    A．[8，10]B．（6，+∞）C．（6，8]D．[8，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

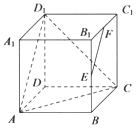    4．如图，在正方体ABCD-A1B1C1D1中，点E，F分别为BB1，B1C1的中点．
    （Ⅰ）求证：直线EF∥面ACD1；
    （Ⅱ）求二面角D1-AC-D的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知直线的方程是$\sqrt{3}x-y+1=0$，则直线的倾斜角是（　　）
    A．120°B．150°C．30°D．60°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．下列函数中，与函数y=ln（x-1）定义域相同的是（　　）
    A．$y=\frac{1}{x-1}$B．$y={（x-1）^{-\frac{1}{2}}}$C．y=ex-1D．$y=\sqrt{sin（x-1）}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．我国古代数学家祖暅是著名数学家祖冲之之子，祖暅原理叙述道：“夫叠棋成立积，缘幂势既同，则积不容异．”意思是：夹在两个平行平面之间的两个几何体被平行于这两个平行平面的任意平面所截，如果截得的两个截面面积总相等，那么这两个几何体的体积相等．其最著名之处是解决了“牟合方盖”中的体积问题，其核心过程为：如下图正方体ABCD-A1B1C1D1，求图中四分之一圆柱体BB1C1-AA1D1和四分之一圆柱体AA1B1-DD1C1公共部分的体积V，若图中正方体的棱长为2，则V=（　　）  
    （在高度h处的截面：用平行于正方体上下底面的平面去截，记截得两圆柱体公共部分所得面积为S1，截得正方体所得面积为S2，截得锥体所得面积为S3，${S_1}={R^2}-{h^2}$，${S_2}={R^2}$⇒S2-S1=S3）
    A．$\frac{16}{3}$B．$\frac{8}{3}$C．8D．$\frac{8π}{3}$

    查看答案和解析>>

    同步练习册答案