
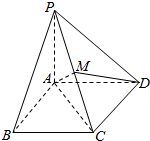
 如图,已知四棱锥P-ABCD中,PA⊥底面ABCD,且ABCD为正方形,PA=AB=a,点M是PC的中点.
如图,已知四棱锥P-ABCD中,PA⊥底面ABCD,且ABCD为正方形,PA=AB=a,点M是PC的中点.分析 (1)建立空间坐标系,求出向量坐标,即可求BP与DM所成的角的大小;
(2)求出平面的法向量,利用向量法即可求二面角M-DA-C的大小.
解答 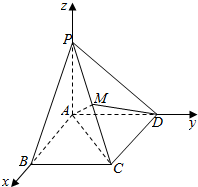 解:建系如图,由已知得A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),P(0,0,a),M($\frac{a}{2}$,$\frac{a}{2}$,$\frac{a}{2}$).
解:建系如图,由已知得A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),P(0,0,a),M($\frac{a}{2}$,$\frac{a}{2}$,$\frac{a}{2}$).
(1)设直线BP与DM所成的角为θ.
∵$\overrightarrow{BP}$=(-a,0,a),$\overrightarrow{DM}$=($\frac{a}{2}$,-$\frac{a}{2}$,$\frac{a}{2}$),
∴$\overrightarrow{BP}$•$\overrightarrow{DM}$=0.
∴BP与DM所成的角的大小为90°.
(2)∵$\overrightarrow{AP}$=(0,0,a),$\overrightarrow{AB}$=(a,0,0),
$\overrightarrow{AD}$=(0,a,0),$\overrightarrow{BP}$=(-a,0,a),
∴$\overrightarrow{BP}$•$\overrightarrow{AD}$=0,$\overrightarrow{AP}$•$\overrightarrow{AB}$=0,$\overrightarrow{AP}$•$\overrightarrow{AD}$=0.
又由(1)知$\overrightarrow{BP}$•$\overrightarrow{DM}$=0.
∴$\overrightarrow{BP}$是平面MDA的法向量,$\overrightarrow{AP}$是平面ABCD的法向量,
则cos<$\overrightarrow{BP}$,$\overrightarrow{AP}$>=$\frac{\overrightarrow{BP}•\overrightarrow{AP}}{|\overrightarrow{BP}||\overline{AP}|}$=$\frac{\sqrt{2}}{2}$.
∴所求的二面角M-DA-C的大小为45°.
点评 本题主要考查空间角的计算,利用建立坐标系,利用向量法是解决本题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
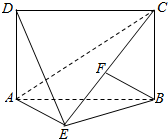 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
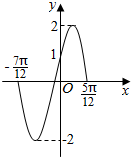
| A. | ω=2 | |
| B. | $f({\frac{π}{3}})=1$ | |
| C. | 函数f(x)的图象关于(-$\frac{11π}{12}$,0)对称 | |
| D. | 函数f(x)的图象向左平移$\frac{11π}{12}$个单位后得到y=Asinωx的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,总有2x≤1 | B. | ?x≤0,总有2x≤1 | ||
| C. | $?{x_0}≤0,使得{2^{x_0}}≤1$ | D. | $?{x_0}>0,使得{2^{x_0}}≤1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
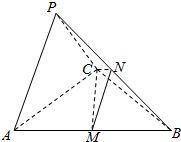 如图,在三棱锥P-ABC中,底面ABC是边长为4的正三角形,PA=PC=2$\sqrt{3}$,侧面PAC⊥底面ABC,M,N分别为AB、PB的中点.
如图,在三棱锥P-ABC中,底面ABC是边长为4的正三角形,PA=PC=2$\sqrt{3}$,侧面PAC⊥底面ABC,M,N分别为AB、PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 0 | C. | -$\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com