
【题目】如图,四棱锥S﹣ABCD的底面是正方形,每条侧棱的长都是底面边长的 ![]() 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点. 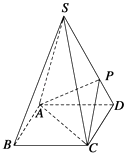
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P﹣AC﹣D的大小.
【答案】
(1)解:连BD,设AC交BD于O,由题意SO⊥AC.
在正方形ABCD中,AC⊥BD,
所以AC⊥平面SBD,得AC⊥SD
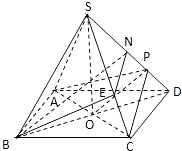
(2)解:设正方形边长a,则SD= ![]() a.
a.
又OD= ![]() a,所以∠SDO=60°,
a,所以∠SDO=60°,
连OP,由(Ⅰ)知AC⊥平面SBD,
所以AC⊥OP,且AC⊥OD,
所以∠POD是二面角P﹣AC﹣D的平面角.
由SD⊥平面PAC,知SD⊥OP,
所以∠POD=30°,
即二面角P﹣AC﹣D的大小为30°
【解析】(1)连BD,设AC交BD于O,则SO⊥AC,在正方形ABCD中,AC⊥BD,根据线面垂直的判定定理可知AC⊥平面SBD,SD平面SBD,根据线面垂直的性质可知AC⊥SD.(2)设正方形边长a,求出SD、OD,得到∠SDO,连OP,根据(Ⅰ)知AC⊥平面SBD,则AC⊥OP,且AC⊥OD,根据二面角平面角的定义可知∠POD是二面角P﹣AC﹣D的平面角,然后在三角形POD求出此角即可.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如表:
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?
资金 | 单位产品所需资金(百元) | ||
空调机 | 洗衣机 | 月资金供应量(百元) | |
成本 | 30 | 20 | 300 |
劳动力(工资) | 5 | 10 | 110 |
单位利润 | 6 | 8 | |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() ,cos
,cos ![]() ),
), ![]() =(cos
=(cos ![]() ,1),且f(x)=
,1),且f(x)= ![]()
![]() .
.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[﹣π,π]上的最大值和最小值及取得最值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ) ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
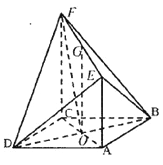
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)当直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,向量 ![]() =(sinα,1),
=(sinα,1), ![]() =(cosα,0),
=(cosα,0), ![]() =(﹣sinα,2),点P是直线AB上的一点,且
=(﹣sinα,2),点P是直线AB上的一点,且 ![]() =
= ![]() .
.
(1)若O,P,C三点共线,求tanα的值;
(2)在(Ⅰ)条件下,求 ![]() +sin2α的值.
+sin2α的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com