
如图,已知四棱锥P—ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD的中点.

(1)证明:PE⊥BC;
(2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.
(1)见解析 (2)
【解析】(1)证明 以H为原点,HA,HB,HP分别为x,y,z轴,线段HA的长为单位长,建立空间直角坐标系如图,则A(1,0,0),B(0,1,0),
设C(m,0,0),P(0,0,n)(m<0,n>0),
则D(0,m,0),E( ,
, ,0).
,0).
可得 =(
=( ,
, ,-n),
,-n), =(m,-1,0).
=(m,-1,0).
因为 ·
· =
= -
- +0=0,
+0=0,
所以PE⊥BC.

(2)解 由已知条件可得m=- ,n=1,
,n=1,
故C(-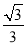 ,0,0),D(0,-
,0,0),D(0,- ,0),
,0),
E( ,-
,- ,0),P(0,0,1),
,0),P(0,0,1),
设n=(x,y,z)为平面PEH的法向量,
则 ,
,
因此可以取n=(1, ,0),
,0),
由 =(1,0,-1).
=(1,0,-1).
可得|cos〈 ,n〉|=
,n〉|=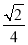 ,
,
所以直线PA与平面PEH所成角的正弦值为 .
.


科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(四)(解析版) 题型:选择题
已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是( )

A.f(b)>f(c)>f(d)
B.f(b)>f(a)>f(e)
C.f(c)>f(b)>f(a)
D.f(c)>f(e)>f(d)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(六)(解析版) 题型:选择题
以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的方程为( )
A.x2+y2+2x=0 B.x2+y2+x=0
C.x2+y2-x=0 D.x2+y2-2x=0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(六)(解析版) 题型:选择题
设集合A={x||x-a|<1,x∈R},B={x|1<x<5,x∈R},若A∩B=∅,则实数a的取值范围是( )
A.{a|0≤a≤6} B.{a|a≤2,或a≥4}
C.{a|a≤0,或a≥6} D.{a|2≤a≤4}
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(五)(解析版) 题型:填空题
已知斜率为2的直线l过抛物线y2=px(p>0)的焦点F,且与y轴相交于点A.若△OAF(O为坐标原点)的面积为1,则p=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(五)(解析版) 题型:选择题
已知抛物线x2=2py(p>0)的焦点F恰好是双曲线 (a>0,b>0)的一个焦点,且两条曲线交点的连线过点F,则该双曲线的离心率为( )
(a>0,b>0)的一个焦点,且两条曲线交点的连线过点F,则该双曲线的离心率为( )
A. B.1±
B.1± C.1+
C.1+ D.无法确定
D.无法确定
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(二)(解析版) 题型:选择题
若f(x)=- x2+bln(x+2)在(-1,+∞)上是减函数,则b的取值范围是( )
x2+bln(x+2)在(-1,+∞)上是减函数,则b的取值范围是( )
A.[-1,+∞) B.(-1,+∞)
C.(-∞,-1] D.(-∞,-1)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(一)(解析版) 题型:填空题
设f(x)=- x3+
x3+ x2+2ax,若f(x)在(
x2+2ax,若f(x)在( ,+∞)上存在单调递增区间,则a的取值范围为________.
,+∞)上存在单调递增区间,则a的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com