考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:(1)直接利用已知条件求解a3,a4的值;
(2)通过已知条件猜想2anan+1+1=(an+1-an)2,然后利用数学归纳法的步骤证明对一切正整数n,2anan+1+1是完全平方数.
解答:
解:(1)由
a2=得,a
3=15,
由
a3=得,a
4=56. …(2分)
(2)
2a1a2+1=9=(a2-a1)2,
2a2a3+1=121=(a3-a2)2,
2a3a4+1=1681=(a4-a3)2,
猜想:
2anan+1+1=(an+1-an)2.下面用数学归纳法证明. …(5分)
证明:①当n=1,2时,已证;
②假设当n=k(k≥2,k∈N
*)时,
2akak+1+1=(ak+1-ak)2成立,
那么,当n=k+1时,由
ak+1=知,
ak+12-1=akak+2,即
ak+2=,
又由
2akak+1+1=(ak+1-ak)2知,
ak+12-1=4akak+1-ak2,
所以
ak+2==4ak+1-ak,
所以
ak+22=4ak+1ak+2-akak+2=4ak+1ak+2-ak+12+1,
所以
(ak+2-ak+1)2=2ak+1ak+2+1,
即当n=k+1时,命题也成立.
综上可得,对一切正整数n,2a
na
n+1+1是完全平方数.…(10分)
点评:本题考查归纳推理以及数学归纳法的证明步骤的应用,考查逻辑推理能力以及计算能力.



 如图,在四棱锥E-ABCD中,AB⊥平面BCE,DC⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=
如图,在四棱锥E-ABCD中,AB⊥平面BCE,DC⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=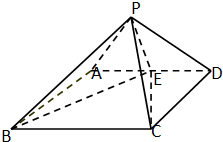 如图,四棱锥P-ABCD的底面是矩形,侧面PAD⊥底面ABCD,在△PAD中
如图,四棱锥P-ABCD的底面是矩形,侧面PAD⊥底面ABCD,在△PAD中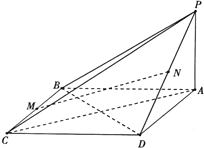 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,M,N分别是BC和PD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,M,N分别是BC和PD的中点.