
分析 先将条件“对任意实数m直线l:x+y+m=0都不是曲线y=f(x)的切线”转化成f'(x)=-1无解,然后求出2sinxcosx+2a=-1有解时a的范围,最后求出补集即可求出所求.
解答 解:∵对任意实数m直线l:x+y+m=0都不是曲线y=f(x)的切线
∴曲线y=f(x)的切线的斜率不可能为-1
即f'(x)=2sinxcosx+2a=-1无解
∵0≤sin2x+1=-2a≤2
∴-1≤a≤0时2sinxcosx+2a=-1有解
∴对任意实数m直线l:x+y+m=0都不是曲线y=f(x)的切线,则a的取值范围是(-∞,-1)∪(0,+∞)
故答案为:(-∞,-1)∪(0,+∞).
点评 本题解题的关键是对“对任意实数m直线l:x+y+m=0都不是曲线y=f(x)的切线”的理解,同时考查了利用导数研究曲线上某点切线方程,以及转化的数学思想,属于基础题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-2,-1)∪(-1,0) | C. | (-∞,-2)∪(0,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平均数为10,方差为2 | B. | 平均数为11,方差为3 | ||
| C. | 平均数为11,方差为2 | D. | 平均数为12,方差为4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{14}{3}$ | B. | $\frac{13}{3}$ | C. | $\frac{3}{14}$ | D. | $\frac{3}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
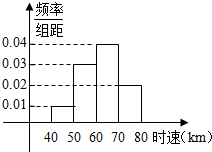
| A. | 60辆 | B. | 80辆 | C. | 70辆 | D. | 140辆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$|⇒$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | |$\overrightarrow{a}$|>|$\overrightarrow{b}$|⇒$\overrightarrow{a}$>$\overrightarrow{b}$ | C. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$|⇒$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=0⇒$\overrightarrow{a}$=$\overrightarrow{0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
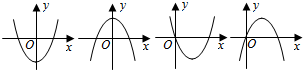
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{5}{3}$ | D. | -$\frac{1}{3}$或$\frac{5}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com