
(本小题满分12分)杭州某通讯设备厂为适应市场需求,提高效益,特投入98万元引进世界先进设备奔腾6号,并马上投入生产.第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元.
请你根据以上数据,解决下列问题:
(1)引进该设备多少年后,开始盈利?
(2)引进该设备若干年后,有两种处理方案:
第一种:年平均盈利达到最大值时,以26万元的价格卖出;
第二种:盈利总额达到最大值时,以8万元的价格卖出.
哪一种方案较为合算?请说明理由.
(1)3年;(2)方案一合算.
【解析】
试题分析:(1)根据利润等于收入-成本,可求利润函数,令其大于0,可得结论;
(2)分别求出两种处理方案的利润,再进行比较,即可得到结论.
试题解析:(1)设引进设备n年后开始盈利,盈利为y万元,
则y=50n-(12n+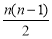 ×4)-98=-2n2+40n-98,
×4)-98=-2n2+40n-98,
由y>0,得10-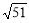 <n<10+
<n<10+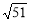 .
.
∵n∈N*,∴3≤n≤17,即3年后开始盈利.
(2)方案一:年平均盈利为 ,
, =-2n-
=-2n-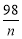 +40≤-2
+40≤-2 +40=12,
+40=12,
当且仅当2n=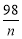 ,即n=7时,年平均利润最大,共盈利12×7+26=110万元.
,即n=7时,年平均利润最大,共盈利12×7+26=110万元.
方案二:盈利总额y=-2(n-10)2+102,n=10时,y取最大值102,
即经过10年盈利总额最大, 共计盈利102+8=110万元.
两种方案获利相等,但由于方案二时间长,所以采用方案一合算.
考点:1.函数模型的选择与应用;2.基本不等式.


科目:高中数学 来源:2015届福建省福州市高三上学期第三次质检文科数学试卷(解析版) 题型:填空题
若函数f(x)为定义域D上的单调函数,且存在区间 (其中a<b),使得当x∈[a,b]时,f(x)的取值范围恰为[a,b],则称函数f(x)是D上的“正函数”,若
(其中a<b),使得当x∈[a,b]时,f(x)的取值范围恰为[a,b],则称函数f(x)是D上的“正函数”,若 是
是 上的正函数,则实数k的取值范围是
上的正函数,则实数k的取值范围是
查看答案和解析>>
科目:高中数学 来源:2015届福建省福州市高三上学期第三次质检文科数学试卷(解析版) 题型:选择题
数列{an},若a1,a2-a1,a3-a2 ,…,an-an-1,…是首项为1,公比为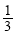 的等比数列,则an=( )
的等比数列,则an=( )
A.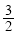 (1-
(1-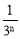 ) B.
) B.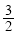 (1-
(1-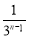 ) C.
) C.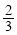 (1-
(1-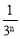 ) D.
) D.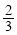 (1-
(1-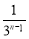 )
)
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高三上学期期中联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知数列 的前
的前 项和为
项和为 ,且
,且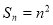
(1)求数列 的通项公式;
的通项公式;
(2)记数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,
,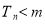 恒成立,求实数
恒成立,求实数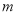 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com