
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对 ;
;
(3)已知函数 是“
是“ 型函数”,对应的实数对
型函数”,对应的实数对 为
为 ,当
,当 时,
时, ,若当
,若当 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围.
(1)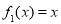 不是“
不是“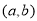 型函数”,理由详见解析;(2)
型函数”,理由详见解析;(2)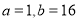 (满足
(满足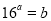 的实数对
的实数对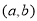 均是正确答案);(3)
均是正确答案);(3) 的取值范围是
的取值范围是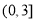 .
.
【解析】
试题分析:(1)根据条件中的描述,若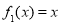 是“
是“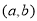 型函数”,则需存在实数
型函数”,则需存在实数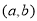 ,使得
,使得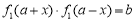 对于任意
对于任意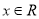 都成立,即
都成立,即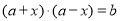 ,
,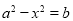 对任意
对任意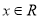 都成立,这显然是不可能的,因此假设不成立,即
都成立,这显然是不可能的,因此假设不成立,即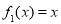 不是“
不是“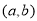 型函数”;(2)根据条件描述,
型函数”;(2)根据条件描述, 是“
是“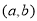 型函数”需存在实数对
型函数”需存在实数对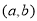 ,使得
,使得 对于任意
对于任意 都成立,即
都成立,即 对任意
对任意 均成立,故所取的实数对只需满足等式
均成立,故所取的实数对只需满足等式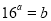 即可,例如
即可,例如 ;
;
(3)根据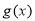 是“
是“ 型函数”可知:
型函数”可知: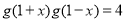 ,即
,即 ,而当
,而当 时,
时, ,故当
,故当 时,若有
时,若有 ,必有当
,必有当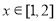 时,
时, ,因此要使当
,因此要使当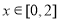 时,都有
时,都有 即等价于当
即等价于当 时,
时, 恒成立,因此可以得到不等式
恒成立,因此可以得到不等式
 在
在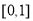 上恒成立,若
上恒成立,若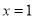 :显然不等式在
:显然不等式在 上成立,若
上成立,若 :参变分离后可转化为转化为
:参变分离后可转化为转化为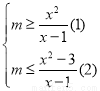 ,显然,当
,显然,当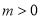 时,不等式(1)成立,而要使不等式(2)成立,
时,不等式(1)成立,而要使不等式(2)成立,
只需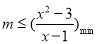 ,通过构造函数令
,通过构造函数令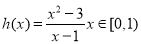 及
及 ,可知
,可知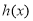 在
在 上单调递增,故
上单调递增,故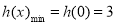 ,因此只需
,因此只需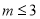 即可从而得到实数
即可从而得到实数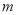 的取值范围是
的取值范围是 .
.
试题解析:(1)假设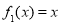 是“(
是“(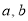 )型函数”,则由题意存在实数对
)型函数”,则由题意存在实数对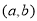 ,使得
,使得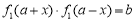 对于任意
对于任意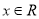 都成立,即
都成立,即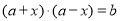 ,
,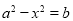 对任意
对任意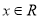 都成立,这显然是不可能的,因此假设不成立,即
都成立,这显然是不可能的,因此假设不成立,即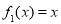 不是
不是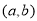 型函数;
型函数;
(2)由题意,若 是“(
是“(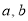 )型函数”,则
)型函数”,则 ,即
,即 ,对任意
,对任意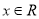 都成立,故所求实数对
都成立,故所求实数对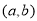 只需满足
只需满足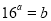 即可,如
即可,如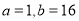 等;
等;
(3) 由题意得: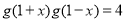 ,即
,即 ,而当
,而当 时,
时, , 故由题意可得,要使当
, 故由题意可得,要使当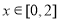 时,都有
时,都有 ,只需使当
,只需使当 时,
时, 恒成立即可,即
恒成立即可,即
 在
在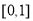 上恒成立,若
上恒成立,若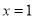 :显然不等式在
:显然不等式在 上成立,若
上成立,若 :则可将不等式转化为
:则可将不等式转化为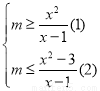 ,因此只需上述不等式组在
,因此只需上述不等式组在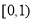 上恒成立,显然,当
上恒成立,显然,当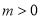 时,不等式(1)成立,令
时,不等式(1)成立,令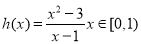 ,则
,则 ,∴
,∴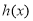 在
在 上单调递增,∴
上单调递增,∴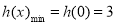 ,故要使不等式(2)恒成立,只需
,故要使不等式(2)恒成立,只需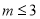 即可,综上所述,所求
即可,综上所述,所求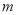 的取值范围是
的取值范围是 .
.
考点:1.新定义问题;2.恒成立问题的处理方法.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:选择题
设离散型随机变量X的概率分布列如下表:
X | 1 | 2 | 3 | 4 |
P |
| p |
|
|
则p等于( )
A. B.
B.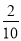 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测文科数学试卷(解析版) 题型:填空题
已知实数x,y满足 ,如目标函数z=x-y最小值的取值范围为[-2,-1],则实数m的取值范围 .
,如目标函数z=x-y最小值的取值范围为[-2,-1],则实数m的取值范围 .
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测文科数学试卷(解析版) 题型:选择题
从椭圆短轴的一个端点看长轴的两个端点的视角为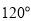 ,那么此椭圆的离心率为( )
,那么此椭圆的离心率为( )
A.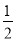 B.
B.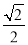 C.
C.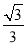 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com