


科目:高中数学 来源: 题型:
| tanC |
| tanA |
| tanC |
| tanB |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
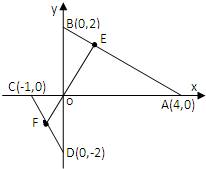 在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.
在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.| OE |
| AB |
| AE |
| EB |
| DF |
| FC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| lge |
| 2 |
| lge |
| 3 |
| lge |
| n |
| (1+n)n |
| nn |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 2 |
| y2 |
| b2 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| y+20 |
| x-10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
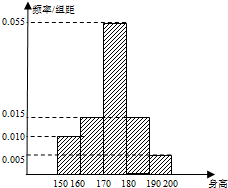 某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.| 身高达标 | 身高不达标 | 合计 | |
| 积极参加体育锻炼 | 60 | ||
| 不积极参加体育锻炼 | 10 | ||
| 合计 | 100 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com