
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 根据题意画出图形,然后对应选项一一判定即可.
解答 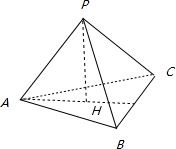 解:∵PH⊥平面ABC,H为垂足.
解:∵PH⊥平面ABC,H为垂足.
∴PH⊥AB,PH⊥AC,PH⊥BC,
①若PA⊥BC,则BC⊥平面PAH,
∴BC⊥AH,同理:AC⊥BH,
则点H是△ABC的垂心,正确;
②若PA,PB,PC两两互相垂直,容易推出AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.
③若∠ABC=90°,H是AC的中点,容易推出△PHA≌△PHB≌△PHC,则PA=PB=PC;正确.
④若PA=PB=PC,易得AH=BH=CH,则H是△ABC的外心,正确.
故正确的命题为:①②③④,
故选:A
点评 本题考查棱锥的结构特征,考查学生发现问题解决问题的能力,三垂线定理的应用,是中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\frac{x+4}{x}$与g(x)=|x2-6x|的定义域为[1,4].
已知函数f(x)=$\frac{x+4}{x}$与g(x)=|x2-6x|的定义域为[1,4].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 正三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com