
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 由于关于x的方程ax2+2x+b=0有实数根,所以分两种情况:(1)当a≠0时,方程为一元二次方程,那么它的判别式大于或等于0,由此即可求出a的取值范围;(2)当a=0时,方程为2x+b=0,此时一定有解.
解答 解:(1)当a=0时,方程为2x+b=0,此时一定有解;
此时b=0,1,2;即,(0,0),(0,1),(0,2),共3种.
(2)当a≠0时,方程为一元二次方程,
∴△=4-4ab≥0,
∴ab≤1.所以a=1,2,此时a,b的对数为(1,0),(1,1),(2,0),共3种,
关于x的方程ax2+2x+b=0有实数解的有序数对的个数为6种,
故选B.
点评 本题考查了一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根,在解题时要注意分类讨论思想运用.考查分类讨论思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [60,70) | ③ | 0.16 |
| [70,80) | 14 | ② |
| [80,90) | 16 | 0.32 |
| [90,100] | ① | 0.24 |
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
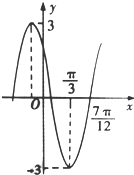 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则曲线f(x)在(0,f(0))处在的切线方程为6$\sqrt{3}$x+2y-3=0.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则曲线f(x)在(0,f(0))处在的切线方程为6$\sqrt{3}$x+2y-3=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com